35.模态空间03.10-为什么有些测量结果有反共振点而有些没有？

MODAL SPACE – IN OUR OWN LITTLE WORLD

模态空间 – 在我们自己的小世界中     Pete Avitabile(著) KSI科尚仪器 董书伟（译）

Oct03-01

为什么有些测量结果有反共振点而有些没有？我们讨论一下这个问题。

2014年04月20日 发布 ver1.0

这个问题问得好。你完全对 – 有些测量结果有反共振点而有些没有。为什么会这样？我们首先讨论一个特殊测量结果，称为驱动点测量结果，接着再延伸这个讨论，来解释测量结果中反共振是怎么发生的。

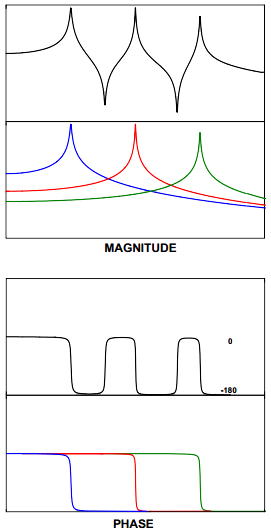
首先解释驱动点测量结果。驱动点测量结果是在同一个点沿同一个方向测量输入力和输出响应。一个典型的驱动点测量结果如图1所示。

 
 
\begin{matrix} h_{ij}=\dfrac{a_{ij1}}{\left ( j \omega-p_{1} \right )}+\dfrac{a_{ij1}^{*}}{\left (j \omega-p_{1}^{*}\right )} \\ \qquad \quad +\dfrac{a_{ij2}}{\left ( j \omega-p_{2} \right )}+\dfrac{a_{ij2}^{*}}{\left (j \omega-p_{2}^{*}\right )} \\ \qquad \qquad +\dfrac{a_{ij3}}{\left ( j \omega-p_{3} \right )}+\dfrac{a_{ij3}^{*}}{\left (j \omega-p_{3}^{*}\right )}\end{matrix}
 
 
 
 
 
 
\begin{matrix} h_{ij}=\dfrac{q_{1}u_{i1}u_{j1}}{\left ( j \omega-p_{1} \right )}+\dfrac{(q_{1}u_{i1}u_{j1})^{*}}{\left (j \omega-p_{1}^{*}\right )} \\ \qquad \quad +\dfrac{q_{2}u_{i2}u_{j2}}{\left ( j \omega-p_{2} \right )}+\dfrac{(q_{2}u_{i2}u_{j2})^{*}}{\left (j \omega-p_{2}^{*}\right )} \\ \qquad \qquad +\dfrac{q_{3}u_{i3}u_{j3}}{\left ( j \omega-p_{3} \right )}+\dfrac{(q_{3}u_{i3}u_{j3})^{*}}{\left (j \omega-p_{3}^{*}\right )} \end{matrix}

Figure\, 1\, - \,Driving\, Point\, FRF(Magnitude,\, Phase,\, Real,\, Imaginary)

对于驱动点测量结果，注意到几点：

    • 在幅频图中所有的共振都由反共振隔开
    • 每经过一个共振点相位降低180度，而每经过一个反共振点，相位增加180度
    • 频响的实部图中，峰一定都指向同一个方向

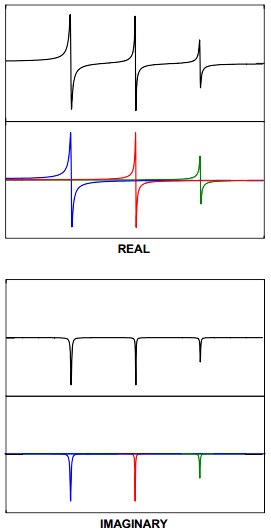
驱动点测量结果可以看作是所有阶模态之和，或者看作每阶模态贡献的结果。在图1的四幅图中，上图含有所有阶模态的和，而下图显示出各阶模态的贡献，对于所示的前3阶模态，频响由描述系统每阶模态的各个单自由度振子之和所组成。作为参考，回想一下，频响可以写成留数或者模态振型的形式，如图1所示。

现在既然明白了驱动点测量结果，可以讨论另外的事情了。例如，频响函数的虚部必然都有相同的方向，在这种情况下每阶模态中间存在一阶反共振。这是因为在反共振频率上1阶模态和2阶模态的频响幅值相等。但在这个频率上，尽管幅值相等，但相位彼此180度反相。这意味着1阶模态和2阶模态相等，而符号相反。因此函数趋向于零。（当各阶模态远离时，如图所示，实际上还有来自其他阶模态的贡献，但通常非常小。）

现在，这意味着当各阶模态的虚部具有相反的符号时，相位不一定反相 – 那么各阶模态加在一起，不会产生反共振。所以每个测量结果可以有反共振或者没有反共振（马鞍状），依赖于频响函数虚部的方向。对相邻模态，当频响函数的虚部具有相同的方向，那么这两阶模态之间存在反共振。当相邻模态的虚部具有不同的符号或方向时，则这两阶模态之间存在马鞍形。

实际上，函数的方向（或符号）与系统的模态振型直接相关。如图1所见，频响函数可以写成留数的形式。但是留数可以按照系统模态振型的形式来表示。当写成模态振型时，由于系统的模态振型，可以很清楚地看出留数的方向符号。图2显示了一个简单的3自由度系统的测量结果。现在观察每个单独的频响测量结果，可以更好地理解频响函数中的相位关系、反共振和马鞍形的出现了。

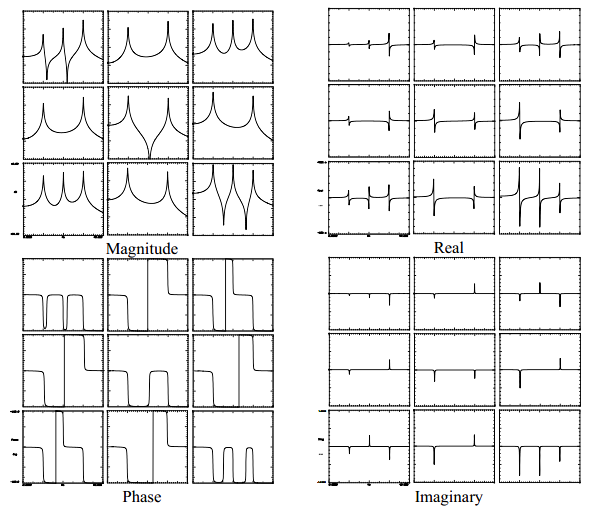
Figure\,2\,-\,FRF\,Matrix\,for\,a\,3\,DOF\,System

我希望这个解释回答了你的问题。如果你有关于模态分析的任何其他问题，尽管问我好了。

burstout

上一篇：34. 模态空间03.08 — 在结构关心部分进行模态测试，很多模态看起来一样！我做错什么了吗？

下一篇：36. 模态空间03.12 — 局部拟合和全局拟合之间有什么区别？

返回模态空间中文翻译目录

ln1px
扩展阅读[new]：
《振动：解析与试验模态分析》辛辛那提大学Randall J. Allemang教授(著) KSI科尚仪器 董书伟(译)...