MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Pete Avitabile(著) KSI科尚仪器 董书伟(译)

局部拟合和全局拟合之间有什么区别?我们讨论一下这个问题
2014年05月31日 发布 ver1.0
这个问题问得好。为了说明这个问题,需要几个简单方程,后面举一个简单的例子来说明区别。我们回忆一下频响函数,它是
有很多“ij”(输出-输入)组合;可能的频响矩阵如图1所示。
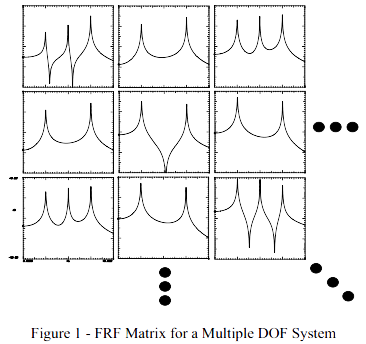
图1 – 多自由度系统的频响矩阵
现在每个频响由极点和留数确定。各个频响都不同,因为留数不同。这个说法是成立的,因为模态振型和留数之间有如下的关系
但是值得注意的是,从一个测量结果到下一个测量结果,频响的分母是相同的,没有发生改变。由于各个测量结果的极点不发生改变,因此可以讲极点是系统的“全局”属性。这表示尽管从一个测量结果到下一个测量结果,留数改变了,但如所期望,极点不变 – 至少在理论上!但是在实际的测量中,情况可能并非如此。实际上,从一个测量结果到下一个,极点可以改变。这会导致问题。
为了理解这点,考虑将要用一条直线拟合的数据,如图2所示。现在,如果只是选择了跟另外一组点(红色)不一样的2个点(蓝色),那么从这两个点计算得到的斜率和y-截距会大为不同。换句话讲,在斜率和y-截距上,存在区别和不一致,取决于用哪些数据来提取参数。当所有的数据按照最小二乘方式一并使用时,得到斜率和y-截距的“最优的”总体估计。
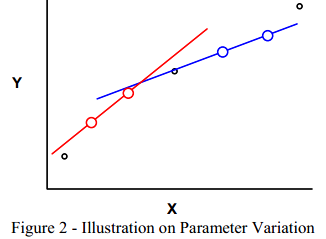
如果不管其他频响而对每个频响进行单独评估,那么从测得的频响进行模态参数的提取中可以看到相同的影响。在估计出的极点中可能有所区别,取决于用哪个频响 – 但是理论指出应该不会产生这种区别。但是当利用实际测试结果提取模态参数,彼此独立地考虑每个测量结果时,这正是实际所发生的。这被称为“局部拟合”。为了避免这个问题,所有的测量结果一并使用,作为一组,以最小二乘方式寻找最优极点,来描述极点的最优“全局”表达。一旦极点估计出来之后,接下来使用模态参数估计方程中的“全局”估计的极点来估计留数。这是一种两步法,在这里首先估计系统的最优“全局”极点,接下来利用估计出来的系统“全局”极点来估计留数,极点没锁定为固定值,而不管每个测量结果可能会标出什么。这即全局拟合。
用一个简单平面框架上的频响测量结果来说明局部拟合和全局拟合之间的区别。几个频响如图3所示。在所示的带宽内有5阶不同的模态。注意上面的2个频响显示出了结构的各阶模态的全部峰,但是下面的2个频响没有含有上面2幅图中每个频率上的所有峰。(这是由于某些测量结果位于某些模态的极点上。)

现在如果在某个特定的测量结果中没有峰,那么怎么能估计出极点值呢?这提出了一个严重的问题,并且正是这些情况,局部拟合失灵了。如果在这种类型的数据上进行局部拟合,那么根据单个频响局部拟合方法估计出来的模态参数可能含有糟糕的提取值,因为极点估计得很糟糕。利用一种局部拟合技术来估计平面框架结构的模态参数。模态振型如图4所示。
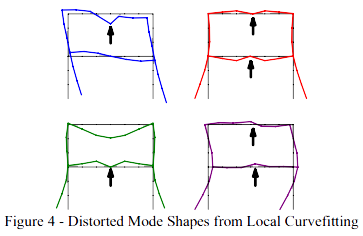
注意,注意在模态振型上有几个位置,数据看上去跟预期的模态振型不一致。模态振型失真了。已经搞清楚,这些点与结构的模态节点相对应。(对局部拟合,这是一个人所周知的问题。)
相同组的频响用于全局拟合。首先,估计系统的最优全局极点,接着在第二步中利用全部频响测量结果的全局极点来估计留数。模态振型如图5所示。注意,这些模态振型是平面框架结构的预期振型。

现在根据这个例子,显然,全局拟合得出更好的结果。但是,当采集数据时,必须小心以保证数据满足全局拟合的要求 – 在所有采集的测量结果中,模态必须是全局的!如果数据不一致,则估计过程中可能会产生误差。必须小心地采集频响数据,满足全局数据缩减过程所需的全局特性。
我希望这个解释澄清了你的问题。如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:35. 模态空间03.10 — 为什么有些测量结果有反共振点,而有些没有?
下一篇:37. 模态空间04.02 — 讨论过模态试验所需测点数。有人告诉我可能无需完全确定整体振型。
![]()
延伸阅读[new]: 《振动:解析与试验模态分析》辛辛那提大学教授Randall J. Allemang博士 编著 KSI科尚仪器 董书伟 翻译…