MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Pete Avitabile(著) KSI科尚仪器 董书伟(译)

你能解释一下互易性吗?对我来说这根本没有意义。
这件事经常让人感到困惑。
2014年05月19日 发布 ver1.0
好吧 – 我们讨论一下模态试验时的测量结果互易性。这是一个非常重要的内容。人们说的话,但有时他们真的不相信它 – 主要因为测量时,为何实际测量结果可能不满足理论的互易性要求是有很多原因的。
我们首先简单地说明一下什么是互易性。图1显示出一幅图,其中,输入-输出测量结果要在点“i”和点“j”进行测量。现在,在一次测量中,在点“i”施加力,在点“j”测量响应。而在第二次测量中,在点“j”测量力,在点“i”测量响应。根据互易性原理,h_{ij}必然等于h_{ji}。
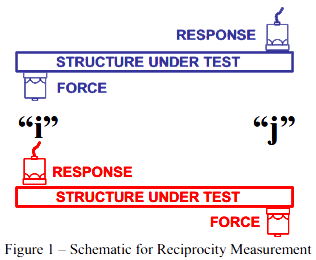
图 1 – 互易性测量的示意图
根据可能的完整测量结果,图2显示了一个频响函数矩阵,其中测量了一行和一列。在这个矩阵中,作为参考,几个互易的测量结果进行了高亮显示。
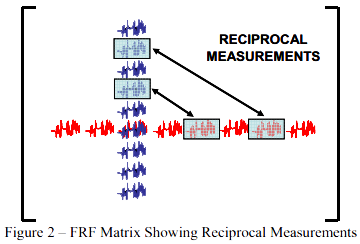
图 2 – 展示出互易测量结果的FRF矩阵
当然,你第一次试图要解释互易性给不熟悉这个概念的人,似乎总是会引起惊讶。所以我们尽量说明,在描述系统的基本方程中互易性是从哪里来的。(为说明互易性,这里必须介绍一些理论)
首先我们知道,我们从写成矩阵形式的多自由度系统的运动方程着手
\left [ M \right ]\left \{ \ddot{x} \right \}+\left [ C \right ]\left \{ \dot{x} \right \}+\left [ K \right ]\left \{ x \right \}=\left \{ F\left ( t \right ) \right \}
现在,这里值得注意的一点是,这些方程是对称的方阵(对结构系统)。这直接说明矩阵的“ij”项和“ji”项是相同的。
现在,对上面写的这个物理运动方程,我们在拉氏域内写。假定初始条件为零,也就是:
\left [ \left [ M \right ]s^2+\left [ C \right ]s+\left [ K \right ] \right ]\left \{ X\left ( s \right ) \right \}=\left \{ F\left ( s \right ) \right \}
当然,我们必须知道这个矩阵的每一项也是对称方阵。根据这个拉氏运动方程,系统矩阵[B(s)]以及它的逆矩阵,系统传递函数
[H(s)],也都是对称方阵。也就是:
\left [ B\left ( s \right ) \right ]^{-1}=\left [ H\left ( s \right ) \right ]=\dfrac{Adj\left [ B\left ( s \right ) \right ]}{det\left [ B\left ( s \right ) \right ]}=\dfrac{\left [ A\left ( s \right ) \right ]}{det\left [ B\left ( s \right ) \right ]}
现在,经过一些运算,系统传递函数可以写成部分分式的形式,作为系统所有各阶单独模态的和。也就是:
\left [ H\left ( s \right ) \right ]=\displaystyle\sum_{k=1}^{m}\dfrac{\left [ A_{k} \right ]}{\left ( s-p_{k} \right )}+\dfrac{\left [ A_{k}^{*} \right ]}{\left ( s-p_{k}^{*} \right )}
频响函数是系统传递函数求s = j \omega 的值,按如下给出:
\left [ H\left ( s \right ) \right ]_{s=j \omega}=\left [ H\left ( j \omega \right ) \right ]=\displaystyle\sum_{k=1}^{m}\dfrac{\left [ A_{k} \right ]}{\left ( j \omega-p_{k} \right )}+\dfrac{\left [ A_{k}^{*} \right ]}{\left ( j \omega-p_{k}^{*} \right )}
现在,重要的是要记住留数矩阵[A(s)]也是对称方阵,因为最终构成它的所有矩阵都是对称方阵。
现在,单个“ij”测量结果可以写成:
h\left ( s \right )_{ij}|_{s=j \omega}=h_{ij}\left ( j \omega \right )=\displaystyle\sum_{k=1}^{m}\dfrac{a_{ijk}}{\left ( j \omega-p_{k} \right )}+\dfrac{a_{ijk}^{*}}{\left ( j \omega-p_{k}^{*} \right )}
并且,展开它的前三阶模态项,得到:
h_{ij}\left ( j \omega \right )=\dfrac{a_{ij1}}{\left ( j \omega-p_1 \right )}+\dfrac{a_{ij1}^{*}}{\left ( j \omega-p_{1}^{*} \right )}
\qquad \qquad \qquad \qquad +\dfrac{a_{ij2}}{\left ( j \omega-p_2 \right )}+\dfrac{a_{ij2}^{*}}{\left ( j \omega-p_{2}^{*} \right )}
\qquad \qquad \qquad \qquad \qquad \qquad +\dfrac{a_{ij3}}{\left ( j \omega-p_3 \right )}+\dfrac{a_{ij3}^{*}}{\left ( j \omega-p_{3}^{*} \right )}
但是,按照这种形式,互易性存在的很不明显。所以需要展开方程的留数形式。回想一下,系统第k阶模态的留数矩阵可以根据奇异值分解得到,写成:
\left [ A\left ( s \right ) \right ]_{k}=q_{k}\left \{ u_{k} \right \}\left \{ u_{k} \right \}^T
或者展开为:
\begin{bmatrix} a_{11k} &a_{12k} &a_{13k} &\cdots \\ a_{21k} &a_{22k} &a_{23k} &\cdots \\ a_{31k}&a_{32k} &a_{33k} &\cdots \\ \vdots &\vdots &\vdots &\ddots \end{bmatrix}=q_{k}\begin{bmatrix} u_{1k}u_{1k} &u_{1k}u_{2k} &u_{1k}u_{3k} &\cdots \\ u_{2k}u_{1k} &u_{2k}u_{2k} &u_{2k}u_{3k} &\cdots \\ u_{3k}u_{1k} &u_{3k}u_{2k} &u_{3k}u_{3k} &\cdots \\ \vdots &\vdots &\vdots &\ddots \end{bmatrix}
并且按照这种形式,很容易写成:
h\left ( s \right )_{ij}|_{s=j \omega}=h_{ij}\left ( j \omega \right )=\displaystyle\sum_{k=1}^{m}\dfrac{q_{k}u_{ik}u_{ij}}{\left ( j \omega-p_{k} \right )}+\dfrac{q_{k}^{*}u_{ik}^{*}u_{jk}^{*}}{\left ( j \omega-p_{k}^{*} \right )}
另外,前3阶模态项可以展开为:
h_{ij}\left ( j \omega \right )=\dfrac{q_{1}u_{i1}u_{j1}}{\left ( j \omega-p_1 \right )}+\dfrac{{q_{1}u_{i1}u_{j1}}^{*}}{\left ( j \omega-p_{1}^{*} \right )} \qquad \qquad \qquad \qquad +\dfrac{q_{2}u_{i2}u_{j2}}{\left ( j \omega-p_2 \right )}+\dfrac{{q_{2}u_{i2}u_{j2}}^{*}}{\left ( j \omega-p_{2}^{*} \right )} \qquad \qquad \qquad \qquad \qquad \qquad +\dfrac{q_{3}u_{i3}u_{j3}}{\left ( j \omega-p_3 \right )}+\dfrac{{q_{3}u_{i3}u_{j3}}^{*}}{\left ( j \omega-p_{3}^{*} \right )}
现在,按照这种形式可以很容易地看出互易性。这是因为留数只不过是第i自由度的模态振型值乘以第j自由度的模态振型值(加上一些其他常数项)。这表示我们在点“i”还是在点“j”测量力,在另一个点测量响应时,这是无关紧要的 – 模态振型在输入和输出位置的值的积是相同的。所以对这种情况,互易性必然发生。举个例子,一个简单的3×3频响矩阵的幅频如图3所示。显然,在矩阵中可以看到互易性。注意实部、虚部和相位也是对称的,但为简洁起见,没有显示。

图 3 – FRF矩阵幅频图
当然,这是理论表示,必然为真。但是,测量结果可能并不总是那么配合。在将来某个时间会讨论这个内容。
我希望这个讨论澄清了所有关于为什么互易性必然为真的困惑。尽管介绍了一些理论方程,但为了说明互易性必然为真,它们是需要的。如果你有关于模态分析的任何其他问题,尽管问我好了。

上一篇:65.模态空间08.10 — 双击不受欢迎,多次锤击又如何呢?
下一篇:67.模态空间09.02 — 我们真的需要精确的修正模型吗?如果它不那么完美有什么影响?
返回模态空间中文翻译目录

延伸阅读[new]: 《振动:解析与试验模态分析》辛辛那提大学教授Randall J. Allemang博士 编著 KSI科尚仪器 董书伟 翻译…




![]()
![]()