MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Pete Avitabile(著) KSI科尚仪器 董书伟(译)

我们总是将试验与完全固支模型进行比较。你真的能在实验室里模拟固支吗?
我们看一看并理解这个问题。
2014年04月25日 发布 ver1.0
这已经成了讨论的惯常话题,只要我还能记事 – 并且随着变老,尽管我可能会忘记某些事情,但这个话题我能记得很好。看起来这个话题总是不断地冒出来引起讨论。当然,这个会发生是因为分析圈子与试验圈子大相径庭的缘故。
在建立分析模型时,我们总是非常简单地确定一个边界条件,加到模型上去。如果想要,我们可以让它完全自由-自由。但是当然,真实世界与分析世界比是大为不同的(分析世界充满了“假设”,在真实世界中那或许就不可能)。
但是至少在自由-自由边界条件下,我们常常可以很好地逼近那个条件。事实上,我们常常愿意按照这种方式进行试验,因为这样的话,对于不是自由-自由的条件,试验装夹方式和相关的试验设置之间少有相互作用。(记住在上篇文章中,一个看上去很不明显的试验设置变化最终是如何导致试验结果产生了非常大的改变。)
问题是,很多时候在部件的连接点,我们愿意用约束的边界条件来验证分析模型。从解析的角度看,这非常可取。但是从实际试验的角度,从各种不同的方面,这是非常复杂的。关于安装面的平面度,螺栓预载荷等等,有着各种各样的问题,这是非常重要的。
但是有一个问题,一个总被误解的问题是,关于产生那个所谓的固支条件,到底硬度要多硬,重量要多重。很多人试图设计“一个无穷刚度”的支撑框架或者试验夹具。但是我们都知道任何结构都会有共振频率,问题只是它们可能发生在什么地方,对于实际产生固支条件的能力可能会有什么影响。对于前面的少数几阶低阶弹性体模态,试验夹具可能是胜任的,但是最终会有夹具共振,可能与试验对象相互影响。
另外一种模拟固支条件的方法是提供一个非常巨大的惯性质量。一般来讲这往往是得到固支边界的更好的办法,但是人们常常不能准确地知道实际上需要多大的质量来达到这个条件。有时,你会听到有人声称惯性质量需要比试验对象的质量大10倍以上。不知什么原因,人们认为10:1这个比值是所有问题的答案。但是我们忘记了,这些“经验法则”要追溯到早期,
那时我们都用计算尺进行计算。在那种精度等级上, 10:1规则或许是一种良好的大概估计。但是目前对于所有这些复杂的模型,在能够求解的条件下,我们真的应该重新考虑那个10:1规则。
为了说明这个问题,用一个类似长梁结构的简单例子来解释。为了得到挥舞模态,我们近期对一个9m的发电机叶片进行了自由-自由试验。相对于惯性负载结合部位来模拟固支条件,这是一个用来讨论的极好物件。
自由-自由情况下测试9m叶片,对前面少数几阶模态的单独挥舞运动,用一个非常粗糙的梁有限元模型来建模这个风电机叶片。目的是为了利用那个自由-自由模型,接着施加一个“完全解析的固支边界条件”,并将它与很多不同的模态进行对比,来研究实际固定叶片到地面所需的质量的数量影响。
作为参考,自由-自由试验和分析模态如表1所示。简单起见,这里没有描述分析模型和所做的试验。
表1 – 9m风电叶片自由-自由条件下的模型和测试结果对比

考虑到这个粗略的梁有限元模型的粗略程度,可以认为这些结果还是不错的。
现在可以用这个分析模型来确定“完全”固支边界条件,并且作为一个参考。同时也将用另一个分析模型来比较增加很大的“惯性质量”到叶片模型根部的影响。这个模型,在不同质量的条件下,将与“完全”参考模型进行对比。将对比频率和振型来说明要得到这个约束条件所需的质量数量的影响。而且非常重要的是注意到质量并不仅仅是一个集中质量,质量具有转动影响。而且对于一个长的悬臂结构,例如发电机叶片,为了建立固支模拟条件,最为重要的影响是这些转动质量的影响。作为参考,发电机叶片重量在400磅量级。用一个66”×72”×24”的厚钢板作为惯性质量的一个近似,它重约22,000 磅,大概比风电机叶片重55倍。
集中质量表示为M,旋转质量表示为MR,在不同的质量、旋转质量比值的条件下,建立了多个模型,并跟“完全”参考模型进行对比,对比得到的模型频率和振型。表2总结了结果,仅仅考虑风电机叶片的第1阶模态;对表2中所示的不同情形,图1展示了振型的比较。
表2 – 9m风电叶片在不同的惯性锚固近似和“完全”固支条件下的对比

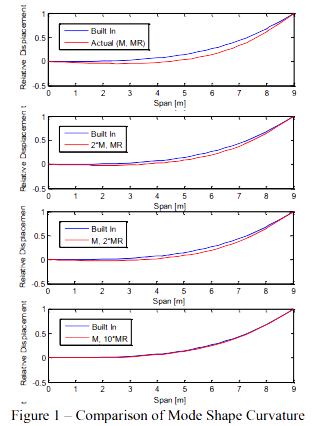
图1 – 模态振型曲率的对比
首先注意到,仅有M和MR作为惯性质量近似的模型没有很好地复现频率;意识到锚固重量比叶片重50多倍。同时也注意到模态振型的曲率跟“完全”参考模型没有很好地吻合起来。现在集中质量加倍,2*M,在相同的转动质量,MR,条件下,表现出一定程度的改善,但仍有差别。另外如果惯量加倍,而集中质量保持不变,结果也近似相同。曲率有改善,但仍有差别。注意到惯性锚固点的旋转质量是使得频率和振型吻合更好的最关键因素。如果转动惯量按照数量级增加,则频率会更好地相关,而且振型的曲率也开始很好地吻合起来。
所以这里首要问题是,为了接近固支条件,惯性质量需要非常大,并且转动质量的影响更为重要,这是因为风力发电机叶片的巨大的悬臂影响。显然具有更低重心的不同结构会有不同的结果,但这个模型的确表明,对于悬臂结构有必要确定惯性锚固点的正确特性,这很重要。
但归根到底,你必须决定距离真正的固支条件多大的变化可以接受;对于所要做的试验目的,多大程度的实际模态振型偏离可以接受。问题是人们常常没有考虑过这些问题,哪怕在任何程度上,因而对于可以接受多大程度的差异,没有明确的说法。如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:85.模态空间12.02 — 某天做了次测试,隔天又做,测量结果看上去不一样。这怎么可能?
下一篇:87.模态空间12.06 — 如果你没有在固有频率上激励结构,那你怎么知道它是什么?
![]()
延伸阅读[new]: 《振动:解析与试验模态分析》辛辛那提大学教授Randall J. Allemang博士 编著 KSI科尚仪器 董书伟 翻译…