93.模态空间13.06-你真的需要测量FRFs吗？或许传递比就可以了吧？

MODAL SPACE – IN OUR OWN LITTLE WORLD

模态空间 – 在我们自己的小世界中 Pete Avitabile(著) KSI科尚仪器董书伟（译）

你真的需要测量FRFs吗？或许传递比就可以了吧？

我们需要讨论一下这个问题。

2014年05月06日发布 ver1.0

在很多情况下，常常测量传递比。这可能是由于在振动台品质试验过程中进行数据采集，在这里，试验对象安装在一个大的振动台上，所有的“被测设备”加速度计测量相对于基础的、施加到试件上的加速度输入。

或者它也有可能是，在运行设备上进行测量，不能测量激振力，只有用加速度计测量的响应结果。当进行飞行试验、汽车测试、悬挂系统测试以及类似试验时，这种情况是非常普遍的。这可能是仅有的数据。但需要注意某些细微的区别。另外非常重要的是，要确认当我们使用所有这些独特的词汇时，我们都使用了相同的术语；有时我发现，名词在不同的行业表示不同的事物，所以核查一下是否理解了定义，总是非常重要的。

所以，先给出几个简单的定义，来解释我们有可能测量的全部结果中的某些差异。如果我们给出下面的定义，

$x(t) \quad$ – 系统的时域输入

$y(t) \quad$ – 系统的时域输出

$S_{x}(f)$ – $x(t)$ 的线性傅立叶谱

$S_{y}(f)$ – $y(t)$ 的线性傅立叶谱

$H(f)\;$ – 系统传递函数

$h(t) \quad$ – 系统脉冲响应

则图1表示线性谱的输入-输出示意图。

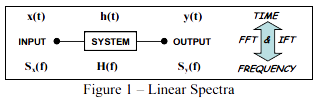
图1 – 线性谱

另外，如果我们给出其他的这些定义，

$R_{xx}(t)$ – 输入信号 $x(t)$ 的自相关

$R_{yy}(t)$ – 输出信号 $y(t)$ 的自相关

$R_{yx}(t)$ – $y(t)$ 和 $x(t)$ 的互相关

$G_{xx}(f)$ – $x(t)$ 的自功率谱 $\qquad \quad G_{xx}\left ( f \right )=S_{x}\left ( f \right )\cdot S_{x}^{*}\left ( f \right )$

$G_{yy}(f)$ – $y(t)$ 的自功率谱 $\qquad \quad G_{yy}\left ( f \right )=S_{y}\left ( f \right )\cdot S_{y}^{*}\left ( f \right )$

$G_{yx}(f)$ – $y(t)$ 和x(t)的互功率谱 $\quad G_{yx}\left ( f \right )=S_{y}\left ( f \right )\cdot S_{x}^{*}\left ( f \right )$

则图2表示功率谱的输入-输出示意图

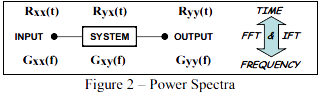
图2 – 功率谱

那么，既然我们已经定义了这些等式，我们就确定一些通常测量的结果，并了解如何用它们计算某些东西，例如，FRF和传递比。

首先要注意的是，线性谱是复数函数，有幅值有相位 – 所以 $S_{x}$ 和 $S_{y}$ 是复数线性谱。但是它们的相伴功率谱， $G_{xx}$ 和 $G_{yy}$ 不是复数的，而是实数的，只有幅值测量结果。这点非常重要，因为没有与之相关的相位信息。但要注意互谱 $G_{yx}$ 是复数，有幅值有相位。

所以我们继续下去，确定FRF和传递比。FRF是互功率谱除以输入功率谱，而传递比仅仅是输出谱除以输入谱。它们如下所示：

H=\dfrac{s_{y}\cdot s_{x}^{*}}{s_{x}\cdot s_{x}^{*}}=\dfrac{G_{yx}}{G_{xx}}\qquad \qquad TR=\dfrac{s_{y}\cdot s_{y}^{*}}{s_{x}\cdot s_{x}^{*}}=\dfrac{G_{yy}}{G_{xx}}

所以尽管我们一般说，这二者都测度输出相对于输入的关系，但有很大的差别 – $FRF$ 是复数的函数，不但有幅值而且有相位，而传递比 $(TR)$ 仅仅是幅值之比；这大为不同，因为没有相位信息。但有一个重要的区别。通常， $FRF$ 用所测的力作为参考进行测量，而 $TR$ 不测量通常需要得到的力。对于模型确认、结构动力学修改、系统模型推导、以及强迫响应研究，当需要数据来求取一个校准的模型时，这一点非常重要 – 可以说，需要测量的力来校准模型。

既然已经完成了所有的定义，那么我们来看一看 $FRF$ 和 $TR$ 的测量结果，来说明一些区别。用简单的自由-自由梁测量一些典型的结果。第一次测量中，用力锤和加速度计进行驱动点 $FRF$ 测量。图3显示了驱动点测量结果的对数幅值和相位；注意这个函数是复数的，如图所示。图4显示了从梁的一端到另一端的跨点测量结果的对数幅值和相位；这个测量结果也是复数值的。