18.模态空间00.12 — 我一直听说SVD，您能为我简单介绍一下吗？

MODAL SPACE – IN OUR OWN LITTLE WORLD

模态空间 – 在我们自己的小世界  Pete Avitabile(著)  KSI科尚仪器 董书伟（译）

Dec00-01

我一直听说SVD，您能为我简单介绍一下吗？当然可以…

我很惊讶你没有更早一些来问这个问题。SVD，奇异值分解可能是最重要的线性代数工具之一，今天我们用它来解决很多结构动力学问题。首先，先介绍一下SVD的数学表达式，以及它的一些变体形式，接着描述一下通常在试验模态分析中它用在什么地方。当然，我会尽量解释SVD的使用及其用途，而不是给出一堆详尽的数学推导。

首先我们必须认识到这里我们要跟矩阵打交道了。（我知道当我们说矩阵的时候，你们都打哆嗦了— 但是我之前就说过“矩阵是你的朋友！”）那么假设我们有某个矩阵[A]，它是一个n \times n的方阵。基本的SVD方程是

\left [ A \right ]=\left [ U \right ]\left [ S \right ]\left [ V \right ]^{T}

现在这个表达式看上去比较简单，但我们将某些项展开来看一看SVD的威力所在

\left [ A \right ]=\left [ \left \{ u_1 \right \} \left \{ u_2 \right \} \left \{ u_3 \right \}\,\cdots\right ]\begin{bmatrix} s_1& & & \\ & s_2& & \\ & & s_3& \\ & & &\ddots \end{bmatrix}\left [ \left \{ v_1 \right \}^T \left \{ v_2 \right \}^T \left \{ v_3 \right \}^T\,\cdots\right ]

将其展开得到

\left [ A \right ]=\left \{ u_1 \right \}s_1\left \{ v_1 \right \}^T+\left \{ u_2 \right \}s_2\left \{ v_2 \right \}^T+\left \{ u_3 \right \}s_3\left \{ v_3 \right \}^T+\,\cdots

现在这真让人难以置信，因为它指出矩阵A由一组向量和奇异值构成，用它们来描述矩阵。

我们从一个简单的向量、一个特征值开始来说明基本的SVD方程。定义向量、奇异值如下

u_1=\begin{Bmatrix} 1\\ 2\\ 3 \end{Bmatrix};\;s_1=1

那么简单地将这些因子乘起来，可得到矩阵A

\left [ A \right ]_1=\begin{bmatrix} 1 &2 &3 \\ 2&4 &6 \\ 3&6 &9 \end{bmatrix}

所以这非常简洁，因为我从一个向量开始，接着构成了一个矩阵。现在这个矩阵显然是一个大小为3 \times 3的矩阵，但我要说它的秩是多少呢？嗯，如果观察矩阵的各个行，我很快会发现第2、3行与第1行线性相关。这意味着尽管我得到了一个3 \times 3的矩阵，但只有一个线性独立信息构成这个矩阵。（我们当然知道这是正确的，因为我们是根据一个向量来构成的矩阵）。我们就可以说这个矩阵的秩是1 — 因为只有一个线性独立信息构成这个矩阵。

现在考虑另外一个简单的向量、一个特征值，如

u_2=\begin{Bmatrix} 1\\ 1\\ -1 \end{Bmatrix};\;s_2=1

那么简单地将这些因子乘起来，可以得到矩阵A

\left [ A \right ]_2=\begin{bmatrix} 1 &1 &-1 \\ 1&1 &-1 \\ -1&-1 &1 \end{bmatrix}

同样，对于这个矩阵我可以做出跟我们之前观察过的第1个矩阵完全相同的注释。这个矩阵的秩是1，因为它是根据一个线性独立信息构成的。

现在，我们考虑一个一般形式的矩阵，如

\left [ A \right ]_3=\begin{bmatrix} 2 &3 &2 \\ 3&5 &5 \\ 2&5 &10 \end{bmatrix}

现在这个矩阵是3 \times 3，但对我来讲，我并不清楚它的秩是多少。确定秩的最简单的方法是对矩阵进行SVD。最后的分解结果是

\left [ A \right ]=\begin{bmatrix} \begin{Bmatrix} 1\\ 2\\ 3 \end{Bmatrix} & \begin{Bmatrix} 1\\ 1\\ -1 \end{Bmatrix} & \begin{Bmatrix} 0\\ 0\\ 0 \end{Bmatrix} \end{bmatrix}\begin{bmatrix} 1 & & \\ & 1 & \\ & & 0 \end{bmatrix}\begin{bmatrix} \begin{Bmatrix} 1 &2 &3 \end{Bmatrix}\\ \begin{Bmatrix} 1 &1 &-1 \end{Bmatrix}\\ \begin{Bmatrix} 0 &0 &0 \end{Bmatrix} \end{bmatrix}

所以SVD的优美之处在于，我可以根据线性独立部分来写矩阵A，线性独立的部分构成矩阵A。这可以按照求和的形式来表示，形如

\left [ A \right ]=\begin{Bmatrix} 1\\ 2\\ 3 \end{Bmatrix}1\begin{Bmatrix} 1 &2 &3 \end{Bmatrix}+\begin{Bmatrix} 1\\ 1\\ -1 \end{Bmatrix}1\begin{Bmatrix} 1 &1 &-1 \end{Bmatrix}+\begin{Bmatrix} 0\\ 0\\ 0 \end{Bmatrix}0\begin{Bmatrix} 0 &0 &0 \end{Bmatrix}

所以我认为这有助于解释SVD的基本原理。但是现在我需要讨论几个通常会用到SVD的应用场合。（SVD有很多不同的应用，但仅专注于与试验测试相关的一些具体应用）

SVD的一个应用是对于试验模态测试，用于MIMO数据的采集。对于所有的MIMO激振器，尽管数据采集系统可能生成不相关的力函数（线性无关），但对每个激振器，实际的激振器激振力或许不能完全无关，这是由于激振器与结构之间存在相互作用造成的。

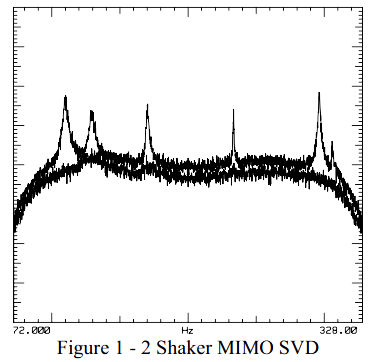
需要检查输入矩阵的线性无关性。在MIMO数据采集的过程中，激振器的G_{xx}可以用来完成通常所谓的主分量分析。这项技术利用SVD将G_{xx}矩阵进行分解，接下来，在频率基础上，画出每个输入对应的奇异值。如果激振器完全线性无关，那么对于每一个独立的输入，在所有频率上都有一个主奇异值。如图1所示。

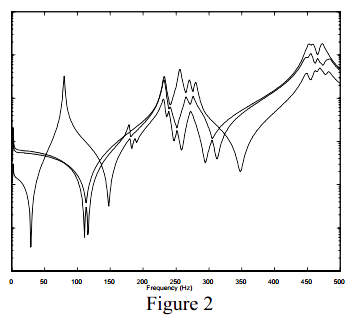
另一个应用是用于模态参数估计。可以利用SVD将不同参考点得到的FRF矩阵进行分解，以确定系统的根（或模态）在什么位置。这种分解是CMIF模态参数估计方法的基础。这个SVD的主奇异值图可以提供图形，用于指示系统模态所在的位置。对有重根的系统，其典型示意图如图2所示。

尽管SVD还有很多其他应用，但我希望这几个例子有助于你更好地理解这项技术。如果你有关于模态分析的任何其他问题，尽管问我好了。

burstout

上一篇：17. 模态空间00.10 — 为什么质量载荷和数据一致性对于模态参数估计是如此之重要？

下一篇：19. 模态空间01.02 — 利用实际工作载荷作为模态试验的激振力有意义吗？

返回模态空间中文翻译目录

ln1px
延伸阅读[new]： 《振动：解析与试验模态分析》辛辛那提大学教授Randall J. Allemang博士 编著 KSI科尚仪器 董书伟 翻译…