力锤对激振能量、带宽的影响分析

董书伟
（北京科尚仪器技术有限公司 北京 100085）

摘要：在对结构进行模态试验时，力锤是重要的激励手段。本文建立了力锤的力学模型，并对力谱进行了分析，指出了在试验过程中使用力锤的注意事项。

关键词：力锤，力谱，试验模态分析

1.简介

在模态试验分析中，需要利用模态激振器或冲击力锤对结构施加一个激振力。力锤激励最重要的优点是不给结构附加任何质量，不会影响试件的动态特性。用力锤输入一个冲激，会产生较为平滑的延伸到指定频率的力。力锤的一般组成如图1所示^[1]。

图1. 力锤组成示意图
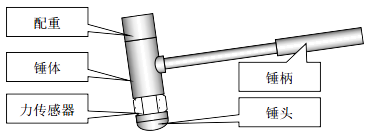
激振力的能量量级和频率带宽取决于力锤与试件接触时的初速度、力锤质量、锤头的硬度以及结构上被敲击点的可塑性（可以刚度来度量）^[2]。

设计力锤的关键环节是锤体质量以及锤头刚度，针对某一特定试验对象选择力锤也是锤击试验中首要考虑的问题，本文针对力锤的锤体质量、锤头刚度对于所能激起的频率范围、激振能量大小进行分析，以对选择力锤有所帮助。

2.力锤力学模型分析

首先力锤及锤头部分可以建模为如下图所示的单自由度系统，锤体（含配重）可建模为集中质量m，锤头建模为弹簧，刚度系数为K。当敲击试验对象时，可假设为此单自由度系统按照一定初速度条件下的自由振动，但这个振动持续的时间段是锤头与被激振物体接触瞬间到锤体反弹开，脱离被激物体的瞬间。

图2. 力锤等效模型
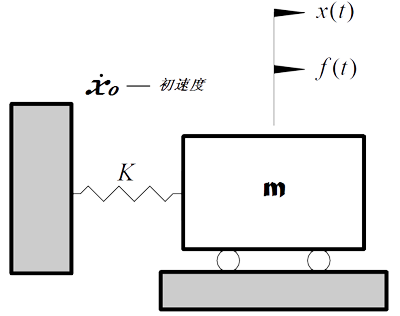
很容易写出其运动微分方程为

m \ddot{x}+K\,x = 0

初始条件如下：t=0，x=0，\dot{x}=\dot{x}_{0}，则上面所示模型的自由运动解为:

x = \begin{cases} \dfrac{\dot{x}_{0}}{\sqrt{\dfrac{K}{m}}} \sin \left ( \sqrt{\dfrac{K}{m}}t \right ) &\text{ } if \; 0 \leq t \leq \pi \sqrt{\dfrac{m}{K}} \\ 0 &\text{ } else \end{cases}

那么其力信号为f = K\,x = \sqrt{Km}\dot{x}_{0}\sin \left ( \sqrt{\dfrac{K}{m}}t \right )

令\tau = \pi \sqrt{\dfrac{m}{K}}，A_{0}=\sqrt{K\,m} \dot{x}_{0}，则上式可写为：

f = A_{0}\sin \left ( \dfrac{\pi}{\tau}\,t \right )

力脉冲的波形为半正弦波形，见图2。

图3. 力信号时域波形

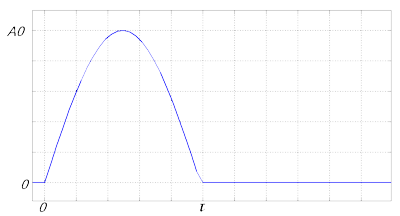
3.力谱分析

对力信号进行傅里叶变换，得力谱

F(f)=\dfrac{4A_{0}^{2}\tau ^{2} \cos ^{2} \pi f \tau}{\pi ^{2}(1-4\tau ^{2}f ^{2})^{2}}

则f=0时，对应其最大值，为

F_{max}=F(0)=\dfrac{4A_{0}^{2}\tau ^{2}}{\pi ^{2}}=(2m\dot{x}_{0})^{2}

令f_{0}=\dfrac{1}{2\tau}=\dfrac{1}{2 \pi}\sqrt{\dfrac{K}{m}}，f_{0}即单自由度系统的固有频率。

其零值处的频率为：

f_{n}=\dfrac{2n-1}{2\pi}\sqrt{\dfrac{K}{m}}=(2n-1)f_{0}

其中，n=2,\,3\, \cdots。

当n=1时，即f=f_{0}时，由洛必塔法则\left ({L}'Hospital \, Rule \right )，

\sqrt{F(f_{0})}=\lim\limits_{f=f_{0}}\dfrac{-2A_{0} \sin \pi f \tau \cdot \pi \tau}{-\pi 8 \tau ^{2}f}=\dfrac{\pi}{2}m\dot{x}_{0}

则

F(f_{0})=(\dfrac{\pi}{4})^{2}\cdot(2m\dot{x}_{0})^{2}

则，力锤所能激起的能量经过f_{0}时，其能量下降了

10log_{10}(\dfrac{\pi}{4})^{2}=-2.1dB

当f=2f_{0}时，

F(2f_{0})=(\dfrac{1}{3})^{2}\cdot(2m\dot{x}_{0})^{2}
则，力锤所能激起的能量经过2f_{0}时，其能量下降了
10log_{10}(\dfrac{1}{3})^{2}=-9.54dB

图4. 归一化力谱曲线

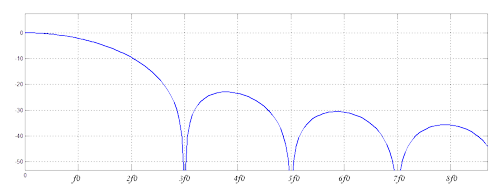
接下来，我们引入如下符号：

令f=\eta \cdot f_{0}=\dfrac{\eta}{2 \tau}，其中\eta \leq 0，\eta=\dfrac{f}{f_{0}}为频率比。

则力谱为

F(f)=\dfrac{4A_{0}^{2}\tau ^{2}\cos ^{2}\pi f \tau}{\pi^{2}(1-4 \tau ^{2} f ^{2}) ^{2}}=\dfrac{4Km\dot{x}_{0} ^{2} \pi ^{2} \dfrac{m}{K}\cos ^{2} \pi \dfrac{\eta}{2 \tau}\tau}{\pi ^{2} \Big(1-4\tau ^{2}(\dfrac{\eta}{2\tau} ) ^{2}\Big) ^{2}}=\dfrac{4m ^{2}\dot{x}_{0} ^{2}\cos ^{2} \eta \dfrac{\pi}{2}}{(1-\eta ^{2}) ^{2}}
=\Bigg(\dfrac{\cos ^{2}\eta \dfrac{\pi}{2} }{(1-\eta ^{2})^{2}}\Bigg)\cdot(2m\dot{x}_{0})^{2}=\Bigg(\dfrac{1-\sin ^{2} \eta \dfrac{\pi}{2}}{(1-\eta^{2})^{2}}\Bigg) \cdot(2m\dot{x}_{0})^{2}
当\eta\rightarrow 0时，F(f) \approx \Bigg( \dfrac{1-(\eta \dfrac{\pi}{2})^{2}}{(1-\eta^{2})^{2}} \Bigg )\cdot (2m\dot{x}_{0})^{2}，可见在低频段能量衰减较慢。

在\eta=0时，根据上式有F(f)=F_{max}=F(0)=(2m\dot{x}_{0})^{2}，结论同前。

当\eta \gg 0时，F(f) \lt \dfrac{1}{\eta ^{4}} \cdot (2m\dot{x}_{0})^{2}，可见在高频段基本已无能量。

4.结论

如上分析可见，力锤所激起的能量与力锤质量、初速度的乘积平方（即力锤的动能）成正比，与频率比有关。一般锤击试验主要靠手工操作完成，精确控制力锤速度比较难于实现。主要依靠调节力锤质量及选择合适的锤头，控制f_{0}。对于频率非常低的超大型结构，重锤轻敲是比较好的办法。

在力锤激励时，能量下降10 \sim 20dB范围的频谱为有效频率，可见有效频率范围主要集中在0 \sim 2f_{0}范围内。通过调整合适的锤体质量、锤头硬度，把主要能量控制在我们感兴趣的频率范围内。

试验经验表明，锤击法得到的脉冲响应函数，其低频部分的相干函数大小主要由f_{0}决定。当激励能量范围太广，即使初速度很大，在低频段相干函数的值仍然很低。

对于大型结构，如要激起更低频率范围内的振动，用更大质量的锤头，更软的锤头来实现。

因此在进行锤击试验时，随身携带不同硬度的锤头，力锤配重，以便灵活调整激振频率范围、激振能量量级。

参考文献

1.《振动结构模态分析—理论、实验与应用》曹树谦 张文德 萧龙翔 天津：天津大学出版社 2001年03月
2.《模态分析理论与实验》 沃德.海伦 波尔.萨斯 白化同（译） 北京：北京理工大学出版社 2001年06月

The effect of hammer on exciting energy level and frequency bands

Abstract：When conducting modal test on a structure, the impact hammer is a good excitation means. In this paper, the hammer is modeled dynamically, the force spectrum is analyzed, and finally, some considerations on how to select a proper hammer are pointed out.

Keywords：impact hammer， force spectrum, experimental modal analysis

备注：原文发表于2010年8月《现代振动与噪声技术》第8卷 p123～126