《振动:试验模态分析》 辛辛那提大学 Randall J. Allemang教授 (著),KSI科尚仪器 董书伟 (译)
目录
1.1 简介
试验模态分析是通过试验的方法确定一个线性、时不变系统模态参数(频率、阻尼因数、模态向量和模态归一)的过程。模态参数可以通过解析的方法,如有限元分析,来确定。试验模态分析的常见理由之一是验证/修正解析方法的结果(模型修正)。虽然解析模型常不存在,但试验方法确定的模态参数可以作为进一步评估的模型,如结构修改。试验模态分析主要是用来解释振动或噪声方面的动力学问题,这些问题从直觉、解析模型或者先前的类似经验方面并不明显。重要的是记住,大多数的振动和/或噪声问题是强迫激励(或初始条件)和模态参数所描述的系统特性二者的函数。单靠模态分析不能解决所有问题,但它在问题解决过程中起着重要的作用。另外,很多振动和/或噪声问题超出了模态分析的假设(例如,线性叠加)。对这些情况,模态分析或许并不是恰当的方法,具体问题具体分析或许更有用。
试验模态分析的历史始于1940年代,工作面向于测量航空器的模态参数,这样就可以精确地预测颤振问题。那时候,测量动态力的传感器原始而落后,方法的模拟属性造成过程耗时而费力,它们在大多数情况下都不实用。随着1960年代中数字小型计算机和快速傅里叶变换(FFT)的出现,开启了试验模态分析的现代化时代。今天,试验模态分析代表了一个交叉学科领域,它融合了信号调理、电子工程的计算机交互、机械理论、振动、声学和机械工程中的控制理论以及应用数学的参数估计方法。
1.2 试验模态分析概述
从试验数据中确定模态参数的过程包括几个阶段。尽管在最简单的情况下,这些阶段可以非常简短,但试验模态分析依赖于对每个阶段基础内容的理解。在大多数的试验情况中,试验模态分析过程的成功取决于对测试情况有非常明确的目标。就减少各阶段的错误而言,这些明确的目标影响过程的每个阶段,尽管有多种方法来划分过程,但这些阶段的一种可能描述如下所示:
- 模态分析理论
- 试验模态分析方法
- 模态数据采集
- 模态参数估计
- 模态数据呈现/验证
模态分析理论指的是经典振动中从理论上解释线性系统存在固有频率、阻尼因数和模态振动的那部分内容。这个理论包括集总参数或离散模型以及连续模型。这个理论也包括作为模态参数可能解的振动实模态及复模态。试验模态分析过程的这个阶段这里不作重复,它们在《振动:解析与试验模态分析》(UC-SDRL-CN-20-263-662)和振动方面的其他教科书中都有总结。振动理论的变换关系对于理解现代试验模态分析方法非常重要。特别是因为模态数据采集阶段常常涉及到离散傅里叶变换,所以模态理论的这方面内容是非常关键的。
试验模态分析方法涉及到所测物理量和经典振动学之间的理论关系,常用矩阵微分方程表示。所有的现代方法都是从矩阵微分方程中提取出来的,不过是根据测量数据生成最终的数学形式。测量数据可以是时域或频域中的原始输入和输出数据,或者经过处理后的某种数据形式,如脉冲响应函数或频响函数。在模态参数估计中,当前大多数方法包含处理后的数据,例如频响函数。总的来说,试验模态分析方法不过是建立起了必须采集的数据形式。
模态数据采集围绕采集数据的各个实际问题,数据是作为模态参数估计阶段的输入所需。因此,必须要小心万分以保证数据符合理论之需以及模态参数估计中所包含的数值算法之要求。这个阶段既包括数字信号处理,又包括构造测量数据(频响函数)。理论要求所关注的事项包括诸如系统线性和系统参数的时不变特性。在此阶段,非常重要的是理解测量过程中的误差来源,包括方差和偏差。某些偏差,肇源于快速傅里叶变换(FFT)的局限性,可能严重影响模态参数的估计结果^{[5-8]}。
模态参数估计关注的是从测量数据中估计模态参数的实际问题,模态参数估计建立在数学模型的选择上,而数据模型的合理性是由试验模态分析方法所保证的。在这个阶段发生的问题大多是由于背离了前一阶段所用到的假设。严重的理论问题,如非线性因素,造成模态参数估计中的严重困难,并且可能是试验模态分析方法完全失效的原因。严重的实际问题,如数字信号处理导致的偏差,将造成类似的问题,但是它们随数据采集技术的变化而变化,可以改变数据采集技术以最大程度地减少此类误差。模态参数估计阶段是试验模态分析过程中所有前期工作误差累积的时刻点^{[9-12]}。
模态数据呈现/验证是指对模态参数提供一种物理显示或解释的过程。例如,这可能就是简单的频率、阻尼、模态振型连同与测量自由度有关的几何结构的数值列表。大多数情况下,模态数据呈现包括画出此类信息的图形及动画。这包含构建一个测试对象三维表示所需的额外信息。首先,这需要含有模态阶次的逐帧动画,其中各自由度连线在一起。模态向量图形或者动画的新方法包括隐藏线计算,它也需要面的定义。
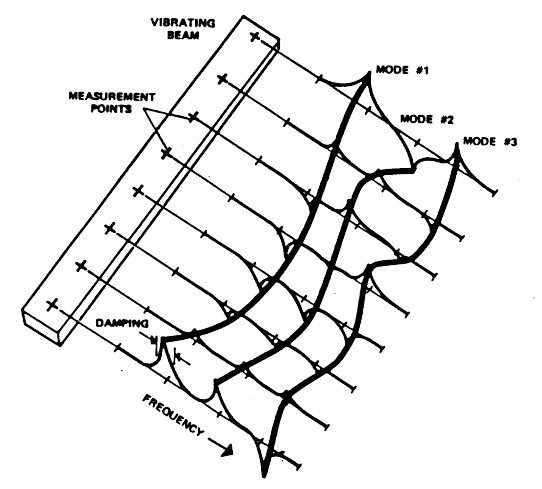
图1-1是这个过程所有阶段的图示。首先,评价一个连续梁的前几阶振动模态。模态分析理论解释说,这是一个线性系统,这个系统的模态向量是实模态。所用的试验模态分析方法是建立在频响函数与运动的矩阵微分方程关系之上的。在每个测量自由度上,此测量自由度与公共输入自由度之间的频响函数虚部垂直叠加于梁上。不用说,本例中的模态数据采集包括所示各自由度的频响函数估计。注意,频响函数是复值函数,并且仅显示了各频响函数的虚部。模态参数估计的一种方法建议:对于小阻尼和各模态之间相邻比较开的系统,频响函数的虚部位于阻尼固有频率上,可以用来作为那个响应自由度的模态系数估计。可以认为频响函数虚部中的正峰、负峰频率是阻尼固有频率。可以根据峰的尖锐程度来估计阻尼。按照这种非常简单的方法已经估计出模态参数。本例的模态数据呈现如连接各峰之线所示。尽管动画也是有可能的,但在这个简单的例子中,单从画图自身中亦能获得模态振型的一种合理解释。
1.3 自由度
在振动领域,包括模态分析中,任何理论概念的发展都取决于对系统自由度(DOF)数目(N)这个概念的理解。对于模态分析领域这个概念是极端重要的,因为一个机械系统的振动模态数目等于自由度数目。从实际的角度来看,自由度数目的理论定义与测量自由度(N_{o},\,N_{i})之间的关系常令人费解。为此,作为模态分析讲义的准备工作,先回顾自由度的概念。
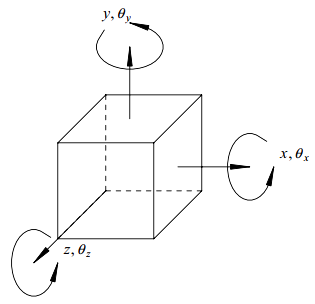
首先,与自由度数目概念相关的基本定义通常包含如下陈述:一个机械系统的自由度数目等于在任意时刻确定机械系统中每个质量的位置及方向所需的独立坐标数目(或最少坐标数)。当这个定义应用于质点时,需要3个自由度,因为要确定质点位置,需要知道质心的x,y,z平动自由度。当这个定义应用于刚体时,需要6个自由度,因为除了需要x,y,z平动自由度之外,还需要\theta_{x},\theta_{y},\theta_{z}转动自由度来确定刚体质量任意时刻的方位和位置。这个概念如图1-2中所示。当这个概念推广到任意一般变形体时,显然可以认为自由度数目是无穷大的。理论上讲这是对的,但一般情况下,尤其是有限元方法,却是将一个一般变形体看作是由非常多的感兴趣的物理点构成的,每个物理点有6个自由度。这样无穷大的自由度数目可以缩减为一个很大但有限的数。
对于一个机械系统自由度数目的理论概念,考虑到测量结果的局限性,理论自由度数目(N)与测量自由度数目(N_{o},\,N_{i})是不同的。对一般变形体,自由度数目(N)最初可以看作是无穷大的,或者如前面章节所讨论,当只考虑有限个感兴趣的物理点时,它等于某个很大的有限数。第一个需要考虑到的测量局限性是,一般情况下感兴趣的分析频率范围是有限的。例如,汽车的大多数主要结构振动模态位于0 \sim 100Hz之间。当考虑这个限制时,感兴趣的系统自由度数现在就从无穷大缩小至一个合理的有限数。下一个需要考虑的测量局限性是测量系统幅值的物理限制。传感器,信号调理以及数据采集系统致使测量结果的动态范围在80 \sim 100dB \, (10^{4} \sim 10^{5})之间。这意味着由于测量仪器的动态范围限制,自由度数进一步减小。最后因为目前几乎没有转动量测量传感器,通常只能测量平动量(位移,速度,加速度,力),因此没有包含转动效应,或转动自由度(RDOF)。总的来说,即使对于一般变形体,感兴趣的理论自由度数被限定为一个比较合理的有限数(N=1 \sim 50)。因此,自由度数目(N)就是感兴趣的振动模态数目。
那么最终测量自由度数(N_{o},\,N_{i})可以定义为测量结果所在的物理位置数目乘以每个物理位置上的测量结果数目。例如,如果一般变形体上的100个物理位置中,在每一个位置都测量x,y和z加速度,那么测量自由度数等于300。显然物理位置的选取是有点任意性的,当然也就没有感兴趣的振动模态的准确信息,所以,自由度数(N)与测量自由度数(N_{o},\,N_{i})之间没有特定关系。一般来讲,为了确定一个机械系统的N阶振动模态,N_{o},N_{i}必须等于或大于N。也要注意到,即使N_{o},N_{i}大于N,也不能保证能从N_{o},N_{i}测量自由度中求得N阶振动模态。N_{o},N_{i}测量自由度必须包含能够唯一确定N阶振动模态的物理位置。例如,在机械系统N阶振动模态的某一阶模态的活动位置中,如果没有任何一个测量自由度处于其上,那么就无法获得此阶模态参数。
在下面章节的单、多自由度内容的推导中,假定存在一组N个的测量自由度(N_{o},\,N_{i}),它允许确定N阶振动模态。现实中,因为没有振动模态的先验知识,N_{o},N_{i}总选的远远大于N。如果这组N_{o},N_{i}测量自由度足够大,并且均匀分布在一般变形体上,则通常可以求得N阶振动模态。
在本书全文和很多其他试验模态参考文献中,将使用频响函数H_{pq}符号来描述通过在测量自由度p施加输入,而在测量自由度p测量响应得到的测量结果。单个下脚标p或q是指位于结构上或处于结构中的沿着特定方向(\pm X,\,Y\,或Z)上的一个物理点。
1.4 基本假设
对于要进行试验模态分析的任何结构,有四个基本假设。
第一个基本假设是认为结构是线性的,也就是说,受到强迫激励任意组合同时作用时的结构响应是每个强迫激励单独作用时结构的独立响应之和。对大多数结构这是一个很好的假设。当结构是线性时,它的行为可以通过受控的激励试验来定性,其中作用到结构上的强迫激励具有易于测量和方便参数估计的形式,而不是类似于在正常运行环境下实际作用到结构上的强迫激励。对于很多重要的结构,线性假设无效。在这些情形下进行试验模态分析,是希望识别出的线性模型提供结构特性的一种合理近似。
第二个基本假设是结构是时不变的,也即,待确定的参数是常数。通常,一个时不变的系统将具有多种部件,它们的质量、刚度或阻尼受到没有测量或者系统中没有包含的因素影响。例如有些部件可能受温度的影响。在这种情况下,部件温度被看作是一个时变信号,因此部件具有时变特性。所以通过任何测量或估计方法来确定的模态参数都将依赖于测量结果的测试时间(受这个温度的影响)。如果待测结构随时间而变化,则试验结束阶段得到的测量结果确定的模态参数不同于试验开始阶段得到的测量结果确定的模态参数。像这样,不同时间得到的测量结果将不一致,违反了时不变假设。
第三个基本假设是结构遵循Maxwell互易性定理,也就是说,在自由度p施加的作用力引起自由度q位置的响应与相同作用力在自由度q施加引起的响应相同。对于频响函数测量结果而言,通过在p点激励、测量q点响应确定的p、q间的频响函数跟在q点激励、测量p点响应确定的频响函数相同(H_{pq}=H_{qp})。
第四个基本假设是结构是可观的,也即,得到的输入-输出测量结果包含足够多的信息,能够生成结构的一个完整特性模型。具有松散部件,或者更一般地讲,具有未测运动自由度的结构和机器不是完全可观的。比如,考虑一个部分充液水箱在发生复杂的液体晃动时的运动。有时在选中的模型形式下,可以得到足够多的测量结果,这样系统是可观的;而有时可行数量的测量结果不能满足需要,除非改变模型。这个假设与下面的事实尤为相干:数据通常描述一个不完备的结构模型。至少在两种不同的情况下这会发生。首先,数据常受到最小频率、最大频率以及有限的频率分辨率的限制。再者,由于转动领域中缺少传感器,与局部转动相关的信息亦不存在。
就待分析的系统而言,可以做些其他假设。通常假设模态参数是全局的。例如,这个假设意味着对于给定的模态频率,每个测量结果中的频率和阻尼信息是相同的。由于测量结果是在不同的时候测量的,而且测试条件也稍有不同,因此对于得到的测量结果,这常不为真。这种情况被称为不一致数据。理论模型并不打算承认这个问题。另一个常做的假设与重根相关。重根是指那种在特征方程中一个复数根(模态频率、特征值、极点等)出现不止一次的情形。具有相同值的每个根含有独立的模态向量或特征向量。这种情况只有通过使用多输入或多参考点才能检测出来。很多模态参数估计算法一次只包含一个测量结果或者一个参考点,因此不能估计重根情形。在推导完整模态模型中,检测重根是非常关键的,这样才可以合成任意的输入-输出信息。尽管理论重根具有商榷意义,但是,相对于测量结果用到的频率分辨率,当两阶模态频率相邻非常紧密时,就存在实际上的重根问题。这种情况是非常现实的问题,称之为伪重根问题。
在涉及实际结构系统的试验测试情况下,这些基本假设从来不会完全符合。一般而言,这些假设近似为真。重要的是要记住,每个假设都可以通过试验的方法来评估,不管是在试验过程中还是完成了试验、已经进行了数据分析之后。进行试验而不做假设有效性的某种测度是不可原谅的。
1.5 参考文献
- Allemang, R.J., Analytical and Experimental Modal Analysis, UC-SDRL-CN-20-263-662, 1994, 166 pp.
- Tse, F.S., Morse, I.E., Jr., Hinkle, R.T., Mechanical Vibrations: Theory and Applications, Second Edition, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1978,449 pp.
- Craig, R.R., Jr., Structural Dynamics: An Introduction to Computer Methods, John Wiley and Sons, Inc., New York, 1981, 527 pp.
- Ewins, D., Modal Testing: Theory and Practice, John Wiley and Sons, Inc., New York,1984, 269 pp.
- Bendat, J.S.; Piersol, A.G., Random Data: Analysis and Measurement Procedures, John Wiley and Sons, Inc., New York, 1971, 407 pp.
- Bendat, J. S., Piersol, A. G., Engineering Applications of Correlation and Spectral Analysis, John Wiley and Sons, Inc., New York, 1980, 302 pp.
- Otnes, R.K., Enochson, L., Digital Time Series Analysis, John Wiley and Sons, Inc.,New York, 1972, 467 pp.
- Dally, J.W.; Riley, W.F.; McConnell, K.G., Instrumentation for Engineering Measurements, John Wiley & Sons, Inc., New York, 1984.
- Strang, G., Linear Algebra and Its Applications, Third Edition, Harcourt Brace Jovanovich Publishers, San Diego, 1988, 505 pp.
- Lawson, C.L., Hanson, R.J., Solving Least Squares Problems, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1974, 340 pp.
- Jolliffe, I.T., Principal Component Analysis, Springer-Verlag New York, Inc., 1986, 271pp.
- Ljung, Lennart, System Identification: Theory for the User, Prentice-Hall, Inc.,Englewood Cliffs, New Jersey, 1987, 519 pp.
![]()
![]()
扩展阅读[new]:
《模态空间系列文章》Peter Avitabile教授 (著) KSI科尚仪器 董书伟 (译)…
《振动:解析与试验模态分析》辛辛那提大学 Randall J. Allemang教授 (著) KSI科尚仪器 董书伟 (译)…