MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Pete Avitabile(著) KSI科尚仪器 董书伟(译)

如果你没有在共振频率上激励结构,那你怎么知道它是什么?
这个问题很重要,要讨论。
2014年04月28日 发布 ver1.0
嗯,我发现这是一个人们经常感到迷惑的地方。很多时候我听到有人说他们需要微调激振频率,这样他们可以恰好在固有频率上的激励,否则将不能正确地识别频率。我还听到有人说激励方法必须在所有频率上具有宽带能量,否则将不能被恰当地激励系统。
有一个错误的想法认为激励频率必须准确地在固有频率上,否则结果无效。嗯,对于做频响试验的方法,以及如何从测得的数据中提取参数来估计系统的频率和阻尼,这真的不是个问题。
所以我们讨论一下这个问题,帮助你理解试验时为什么真的没有必要准确地在固有频率上激励结构 – 但是我们必须保证采集的数据是好的,因为除了好数据之外,别无替代。
现在,我们大体回顾一下一些东西,它稍为简单而且易于被大多数人所理解。我们来看一条非常简单的拟合测试数据的直线。对图1所示的数据,我们要进行平方误差最小化的工作。现在我们知道对数据可以拟合任意的曲线,但对于这组数据,看上去一阶拟合更有道理。当然,我们要用到模型是
有两个参数确定这条直线,也就是斜率和y截距。
数据及数据的拟合如同1所示。现在仔细观察这个数据。我们知道可以计算斜率,但是我们真的曾经测试过斜率吗?真的没有 — 我们测量数据,然后用一个数学函数去拟合那个数据,接下来再用它得到斜率 – 但从技术上讲,我们没有测量斜率。下面再看看y截距。如果仔细观察,你会发现我们从来没有测量直接得到y截距的数据。但无疑我们可以说我们能够得到y截距,但我们真的从来没有实际去测量它,不是吗?我们再稍稍进一步来看看如果对于给定的x值,我们可以得到y函数的值,比如说0.707。但对于那个特别的x值,我们从来没有实际去测量这个函数 – 但我们可以说,根据我们拟合的函数,我们知道它将会是什么。我认为对于这些说法以及我们得到的值,我们都很坦然 – 是吧?
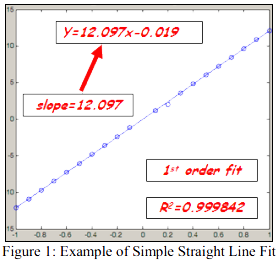
图1 – 简单的直线拟合示例
所以现在我们将这个逻辑加到用来代表单自由度频响函数的数学函数上。对这个单自由度系统,可以按照部分分式的形式写出系统传递函数,形如
并且也可以将频响函数写成
首先需要认识到,这个函数是写成频率的函数,它包含2个常数,极点,p,留数,r;它们是我们需要提取的两个参数(就如同对于直线,我们对斜率和y截距做的那样)。现在我们可以在一系列delta f间隔的频率上求这个函数的值。如图2所示。当测量频响函数时,这些数据点是我们采集的。我们可以对这个数据拟合一条曲线并提取感兴趣的参数,其中这条曲线是复值频响函数。
这里对频响函数,我可以下相同的结论,这个结论对于直线已经下过。对测得的数据我们要拟合一条曲线,并提取定义那条曲线的几个关键参数。它们也就是极点和留数。就如同对于直线我们讨论的那样,为了得到极点或留数的估计,我不需要一个准确地位于固有频率上的数据点。只要我有代表这个函数的良好数据就可以了,对测得的数据,可以拟合这个简单的单自由度模型来提取感兴趣的参数,它们是极点和留数。
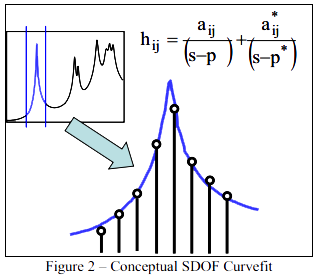 图2 – 概念的单自由度拟合
图2 – 概念的单自由度拟合
现在我当然可以将这一点从单自由度系统扩展到多自由度系统,并且只是问题在数学上变得更为复杂一些罢了 – 但总体上讲这是相同的过程。一个多自由度频响函数测量结果如图3所示。
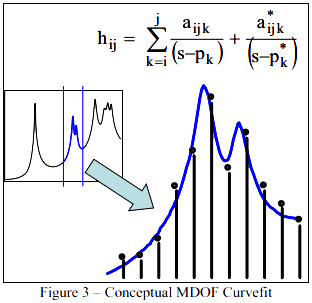
图3 – 概念的多自由度拟合
按照选定的频率间隔采集数据,并且对于从参数估计过程中获得模态,没有必要保证频率数据点正好跟精确的固有频率一样。但确定无疑我必须提醒各位,为了提取留数和极点,必须用最好的测量方法得到采集的数据,以保证在采集的数据和用来描述数据的曲线之间的误差很小。
所以我希望这一个不太多的解释有助于搞清这个事实,测量数据没有必要正好处在系统的精确固有频率上。模态参数估计过程(实际上它不过是一个非常精巧的平方误差最小化的过程)可以提取这些参数,也就是极点和留数。如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:86.模态空间12.04 — 我们总是将试验与完全固支模型对比。真的能在实验室里模拟固支吗?
下一篇:88.模态空间12.08 — 一个试验需要何等自由?多等自由真的至关重要吗?
![]()
延伸阅读[new]: 《振动:解析与试验模态分析》辛辛那提大学教授Randall J. Allemang博士 编著 KSI科尚仪器 董书伟 翻译…






