MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Pete Avitabile(著) KSI科尚仪器 董书伟(译)

我还是搞不清MAC?什么是“好”的MAC值?现在我将要告诉一些你可能不想听的事情!
2016年06月06日 发布 version1.0
我发现很多人对理解和接受这个问题有困难。大多人都有可能像鸵鸟那样“把头埋在沙里”,装作看不见,希望问题会消失。嗯…这里我要展示一些很多人接受起来有困难的东西。但是,首先让我从几个与相关和正交相关的词语开始,因为这二者之间存在着巨大的差异,很多人可能会认为模态置信准则(MAC)跟正交性检查是一回事 — 但实际上它们大为不同。
例行公事,描述MAC和正交性的两个公式分别是:
首先要指出的是,MAC实际上不过是归一化的矢量点积,在0到1之间取值。如果MAC值接近于0,那么我们说这两个矢量之间不相关。如果MAC值接近于1,则两个矢量非常相似。但是你注意到从来就没有用正交这个词。只是用了相似这个词。
现在,正交性是一种数学属性,产生于描述系统质量和刚度矩阵的特征解。特征解的一个副产物是,矢量“线性独立”,矢量“关于质量和刚度矩阵同时正交”。所以正交性是一种属性,由特征解的结果所保证成立。对那个计算,MAC不做这样的保证。
正交性检查是执行的一种更为严格的检查,在航天航空和军事应用中,它时常被强制规定作为认证过程中的一部分。解析/有限元模型的模态振型常常与试验测得的矢量进行比较。管理机构规定相似矢量的质量正交性必须大约90%或95%,不同矢量的值必须不高于5%到10%。也就是说,质量正交矩阵的对角元素必须大于90%,而所有非对角元素必须低于10%。现在这些行业中,MAC通常不再用于模型的验证,因为正交性是一种更好的相关标识符。
在其他行业又如何呢?嗯,确实没有一家授权或管理机构,所以很多时候公司或行业有普遍遵循的“良好习惯做法”。MAC实际上产生于试验环境,其中试验工程师想要确定从某一次试验测得的振型跟下次得到的振型是否相似,或者一个原型跟一个产品配置是否一样,或者…(等等不一而足,在很多情况下,我们可以使用MAC)。
那么他们为什么不使用正交性检查呢?嗯,记住,MAC出自试验人员,可追溯到30-40年前,试验人员没法得到质量矩阵;只有一些分析工程师可以使用非常原始的有限元建模工具。加之MAC易于计算。不管怎么说,他们没有质量矩阵,又不想耗神费力于更为复杂的质量正交性检验。试验人员就想做点简单的比较。
但接下来所有事情“水到渠成”,突然地,我们有人使用MAC将有限元模态振型和测得的试验数据关联起来。并且突然地,我们有人使用MAC对模型进行相关性验证,接着他们开始使用正交性检验所发展起来的某些相同的一般准则。
但我经常地会听到有人讲,他们可以接受低于90%的相关向量MAC值,有时候接受低至80%的相关值,因为“我们正在打交道的是实际结构,而不是简单的学术范例”。嗯,我并不完全肯定我赞成这种想法,因为在MAC计算中没有包含质量矩阵。
我想展示两个例子来说明某些MAC值,它们是从显然完全不同的模态得到的。第一个例子是来比较一个自由-自由梁的摇摆刚体模态和悬臂梁的第一阶模态。图1所示,MAC值指出有大约60%的相似性。
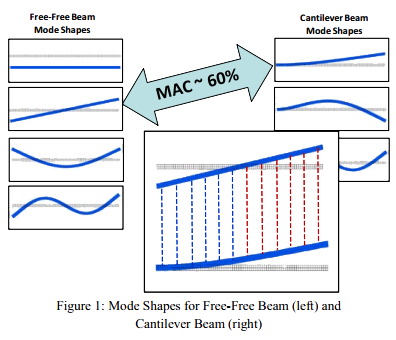
图1:自由-自由梁(左侧)和悬臂梁(右侧)的模态振型
亲爱的莫莉小姐!这两个向量彼此没有什么关系,但是MAC显示出了60%的相关。那怎么可能发生呢。嗯,如果你观察图1右下方的插图,可以看到从根部到梁跨中的悬臂梁模态振型值非常小,MAC值计算中它们的贡献很小。另外如果你观察梁从跨中到顶部的振型,值要大得多,并且你用肉眼也能看出摇摆刚体模态看上去非常相似。这就是MAC所指示的。但是我们知道这两阶模态根本就不一样。现在你可能争解我没有权利比较这些模态,但我只是为了展示60%MAC指出了什么。那是多么离奇啊!!!!!
现在让我们拿两个悬臂梁继续下去 — 一个是质量均匀分布的,另一个在梁中部有一个附加的集中质量块(梁重量的20%)。现在如果我观察质量均匀分布梁的1、2阶模态之间的MAC,跟预料一样,MAC将显示极小相关。但是当在附加集中质量块的梁上计算MAC时,1、2阶模态之间的MAC几乎是80%。莫莉小姐根本就不信这点。但是如果你观察图2右上部均匀分布梁的模态,将它们与图2右下部的模态进行比较,你开始看到相同的情况,跟第1个例子中讨论的一样。靠近支架根部的模态振型值对MAC的贡献很小。1、2阶模态的梁根部的振型值看上去非常相似。这就是MAC再一次所指出的。但我们知道这两阶模态相互正交,但在这里MAC完全失灵。但是,质量正交性清楚地识别出了向量的状态,因为在正交性检查中包含了恰当的质量贡献。对这种情况,MAC没有办法计入不均匀的质量分布。
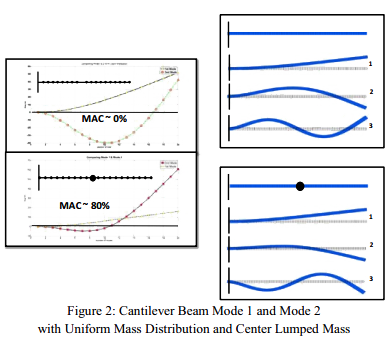
因此我希望你能明白MAC值可能具有欺骗性。MAC没有质量矩阵。这是它的最大优点,同时也是它的最大缺点。现在你不要误会…我一直用MAC来帮助整理模型和试验结果。但当据认为是“相关的模态”的MAC值没有很大的指标时,我是非常质疑的。
我希望这有助于解释清楚你的问题。我们可能会在将来的文章中更多地讨论一下MAC。如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:99.模态空间14.06 — 你测试求频率时重力起作用吗?朝向有影响吗?
下一篇:101.模态空间14.10 — 建立自由-自由试验设置的最好办法是什么?因为没有什么是真正自由-自由的。
![]()
扩展阅读[new]:
《振动:解析与试验模态分析》辛辛那提大学 Randall J. Allemang教授(著) KSI科尚仪器 董书伟(译)…