MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界 Pete Avitabile(著) KSI科尚仪器 董书伟(译)

锤击试验时,加指数窗会带来什么问题吗?
那我们就讨论一下这个问题吧。
如果指数窗使用不当,会带来某些问题。如果需要过大的阻尼来减少泄漏的影响,那么你要承担丢掉密集模态的风险。这里用多个例子来说明关于窗函数的使用,以及如果没有合理使用指数窗会发生什么情况。
首先,我要清晰地表明我的观点:很多冲击试验情况下,有必要使用指数窗。但是,在施加任何窗函数之前,还是要尝试其他办法来减少测量结果中的泄漏为好。在施加阻尼窗之前,增加谱线条数或者带宽减半是两件总要研究的事情。这两种情况实质上将增加采集数据的总时间。这通常有助于允许系统的响应在采样周期结束之前自然衰减到零。如果这样,就没有必要用指数窗了。
但是,如果在采样周期结束的时候,响应仍然没有衰减到零,那么指数窗是有必要的。采取前面两项措施(上面提到过的)作为可能的方法来减少泄漏问题以后才可以施加指数窗。不先观察时域响应就随意使用指数窗作为测量过程的第一个步骤是不推荐的。让我们通过简单例子来考察这个问题。
对一个非常简单的,小阻尼结构进行锤击测试。400Hz带宽选作信号处理参数,最后得到1.0秒的时间窗。由于这个结构预计在采样时段结束的时候还有响应没有衰减到零,施加指数窗,这样加窗后的响应在采样时段结束的时候应该衰减到一个非常小的数值,这样就减少了泄漏的影响。锤击激励、加窗后的指数衰减响应以及频响函数如图1所示。这个测量结果表面上看起来可以接受。[注意输入谱(没有显示出来)在整个频率范围内相当平坦,这样可以充分激励起这个结构。另外也注意到相干(没有显示出来)也认为是非常可以接受的。]
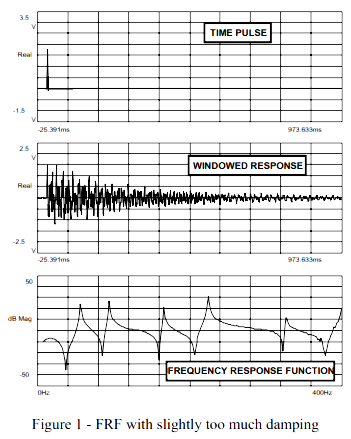
从各方面来看,这个测量结果看上去很让人接受。但我们需要从更深的层次上来观察这个测量结果。首先,我们考虑相同的测量结果但是添加更大的阻尼到响应信号中去。图2显示了相同的数据,但是指数窗的阻尼值更大。与图1中所示的频响相比,这个信号的锤击测量结果得到的频响很明显地具有更大的阻尼。频响的峰值表明了这种影响;注意因为阻尼窗的过度使用,峰更宽了。
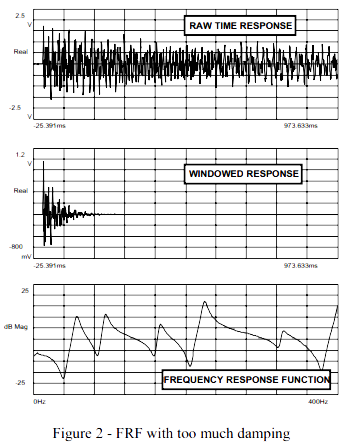
现在,我们更深入地探究一下这个测量结果,并且尝试一些可能的信号处理参数。为了不用阻尼窗,要么减少带宽要么增加谱线条数。这二者的改变最终都增加了采集样本数据所需的总时间。如果总时间增加了,那么就不那么需要对采集的时域数据施加大的阻尼窗了。
图3显示了谱线/时间条数增加一倍的情况。时域样本点从1.0秒增加到2.0秒。尽管仍然需要一个指数窗来减少泄漏,但是加到测量结果上的总体阻尼影响远小于前面图1和图2中所示的测量结果。
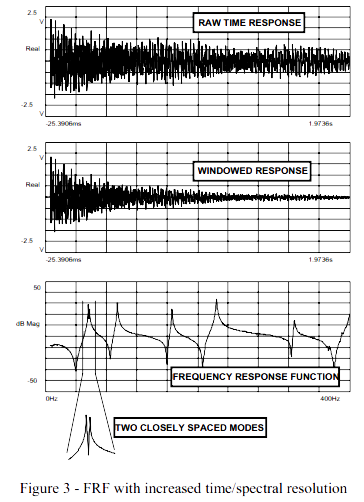
图3中最需要注意的一点是频响函数中在第一个峰附近看上去像是一阶模态实际上是结构的两阶紧邻模态。图1和图2中加指数窗的结果是在频响函数第一个峰附近看上去像是只有一阶模态。阻尼窗的使用导致了完全不同的两阶模态在频响函数中看起来像是只有一个峰。
尽管需要阻尼窗来减少泄漏,但是窗函数使得图1和图2 中的实际频响函数发生了失真,以至于难以观察在这个频率附近存在的两个峰。尽管从信号处理的考虑来看,是需要使用指数窗的,但是当评价如本例所示的小阻尼结构以及密集模态的时候,它也带来一些很大的麻烦。
好了,我希望你能理解本例中指数窗的某些影响。尽管或许需要指数窗来减少泄漏的影响,但是窗函数的使用也可能导致测量结果中的模态丢失或者失真。进行锤击试验使用窗函数时,非常小心是极其重要的。如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:19. 模态空间01.02 — 利用实际工作载荷作为模态试验的激振力,有意义吗?
下一篇:21. 模态空间01.06 – 用多参考点有什么好处吗?我原以为只需要一个参考点。
![]()
扩展阅读[new]:
《振动:解析与试验模态分析》辛辛那提大学Randall J. Allemang教授(著) KSI科尚仪器 董书伟(译)…