MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Pete Avitabile(著) 董书伟(译)

用多参考点有什么好处吗?我原以为只需要一个参考点。
那我们讨论一下这个问题吧。
这是个很好的问题,是一个从试验数据中估计模态参数常常会遇见的问题。根据模态分析理论,我们很容易说明为了估计一个系统的所有阶模态,只需要一个参考点 — 至少从理论的角度来看!尽管从理论上讲这是正确的,但是从实际的角度来看,很多情况下非常需要多个参考点。在我们能够理解这点之前,让我们看一看一些基本概念,这样将有助于说明我们可能会遇到的某些问题。
我们拿一个简单的结构开始这个讨论,这个结构的模态振型实际上非常具有方向性。我们在之前的其他讨论中曾经用过这个结构(5月/6月2000年,Vol.24,No.3)。结构的前几阶模态如图1所示。
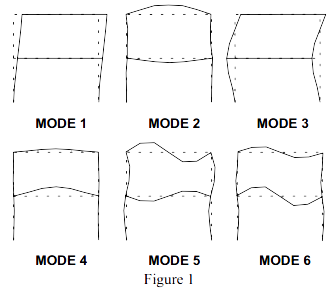
在结构的前6阶模态带宽范围内,如果我们沿垂直方向观察一个参考点,注意到在测得的频响函数中只能看到2个峰。并且如果我们沿着水平方向取一个参考点,同样注意到只有4个峰。但是如果对测量结果更仔细地审视,我们会注意到每个测量结果的前2阶频率是不同的。
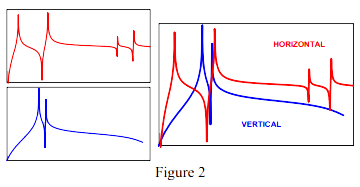
我们重写频响函数的公式如下
总的来说,这个公式根据留数(在分母中)和极点(在分子中)来描述系统的各阶模态。我们必须记住对于任意一个感兴趣的输入-输出组合,都可以写出这个频响函数。现在这个公式有意思的一点是尽管留数是变化的,它取决于用哪一个输入-输出组合,而极点却并不变化。这表明系统的极点是全局性的。它们与特定的输入-输入点无关。但是实际上留数却确实会发生变化。
那么当进行模态试验时,通常情况下是相对于一个特定的参考点采集所有的测量结果。典型情况是,要么当进行激振器激励时激励位置固定,要么进行锤击试验时加速度位置固定。所以相对于某个特定的参考点,采集到的测量结果将含有留数,如下所示
在这种情况下,参考点是“1”,因为所有的留数都是相对于那个自由度的。留数是a_{11},a_{12},a_{13}等等。(注意,下标“k”用于表示系统的某一阶特定模态。)
我们也要记住留数与模态振型(以及一个比例因子)直接相关,如下所示
这意味着留数实际上与系统的模态振型直接相关,如下所示
注意到点1位置的参考自由度可以作为因子提取出来,因为对于所有的测量结果,它是相同的。如果这么做,情况就非常明显了,对于留数的幅值参考自由度起着极端重要的作用;这直接关系到频响函数的幅值。对于某一阶模态,如果参考点位于结构上的模态振型响应非常小的位置,那么对于这阶模态来讲,频响函数的幅值同样也非常小。另一方面,如果参考点位于一个模态振型响应非常大的位置,那么频响函数的幅值也会非常大。
当然,我们接下来也可以看到,如果参考点位于一个自由度上,其中对某一阶模态,振型值非常大,而对于另一阶模态,振型值又非常小,那么频响函数的幅值将具有同样的性质。这是一个进行任何模态测试时的普遍问题。我们总要尽量把传感器布置在一个位置,其中在关心的频率范围内,可以看到所有阶模态具有相同的幅度。但很多情况下,这通常是非常困难的,几乎不可能。
但是对于种情况,我们可以利用频响函数矩阵的某种冗余性来帮忙。如果我们观察这个矩阵的某些项,可以注意到一些有趣的事情。作为参考展开留数矩阵的某些项,如下所示
注意到在这个矩阵中是具有冗余性的。每一列都包含有信息,它与系统的第k阶模态振型相关,并乘以参考自由度。(同样注意到,因为对称性,各行也包含有相同的信息。)这个非常重要的事实就是为什么很多模态参数估计算法要利用多参考点模态试验数据的原因。对于某一阶特定的模态,每个参考点都包含了相同的基本信息,只不过是由参考自由度进行了比例化。因此,可以提取这种冗余信息并用于曲线拟合过程。
更重要的是,如果某个参考点没有很好地激发起某一阶特定模态(例如,参考点靠近那阶模态的节点位置),那么或许还有其他的参考点,它们位于更好的参考位置,以确定那阶模态。所以,利用多参考点就减少了绝对性把握的要求,这个要求是仅从一个参考位置就可以相当好地激起系统的所有阶模态。为了利用所有的参考点数据来提取有效的模态参数,模态参数估计过程利用所谓的模态参与因子的加权项。因此利用多参考点数据对于确定模态参数是极其有帮助的。使用冗余数据允许选择多个参考点,其中的每一个参考点对系统的某些模态是很好的,但不是对所有模态都好。但是,利用多参考点允许综合各参考点来充分描述所有阶模态。如此一来,多参考点提供了充分确定系统所有阶模态的最大可能机会。仅利用一个参考点或许就不是完全可能 – 尽管理论上讲,也是有可能的!
我希望这个解释有助于你们理解为什么多参考点尽管不是理论上必须,但是大有好处。如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:20. 模态空间01.04 — 锤击试验时,加指数窗会带来什么问题吗?
下一篇:22. 模态空间01.08 – 锤击试验时,要考虑的最重要的事情是什么?
![]()
延伸阅读[new]: 《振动:解析与试验模态分析》辛辛那提大学教授Randall J. Allemang博士 编著 KSI科尚仪器 董书伟 翻译…