MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Peter Avitabile(著) KSI科尚仪器 董书伟(译)
你能为我解释模态分析吗?
嗯…说来有点话长,但下面的解释人人都可理解
请我用简单的概念来解释模态分析,以便任何人都可以理解它,你不是第一个人。简言之,模态分析是一种方法,籍此,可以根据结构的频率、阻尼和振型等固有属性-其动态特性-来描述结构。这真够拗口的,那我们来解释这是什么意思。不钻技术牛角尖,我经常用一个简单平板的振动模态来解释模态分析。对于刚接触振动及模态分析的工程师们来讲,这种解释向来有益。
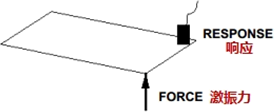
考虑一个自由支撑平板,施加常力于平板一角。我们通常从静态的意义上来看待一个力,它在平板内引起某种静态变形。但这里我要做的是施加一个按正弦方式变化的力,振荡频率固定的常力。我们将改变振荡频率,但不改变力的峰值-仅是力的振荡频率改变。另在平板一角安装一加速度计来测量激励引起的平板响应。
如果现在测量平板响应,注意到当改变输入力的振荡频率时,响应幅值也发生变化。频率升高过程中,不同时刻点上,幅值有增也有减。这好像很奇怪,因为我们施加常力于系统,响应幅值却随输入力的振荡速率而变化。但这确确实实发生了 — 当施加的力的振荡速率越来越接近于系统固有频率(或共振频率)时,响应增大,当振荡速率为系统固有频率时,响应达到最大值。想想看,这真令人惊奇,因为我每时每刻都施加了相同幅值的力-仅仅是振荡速率改变而已!
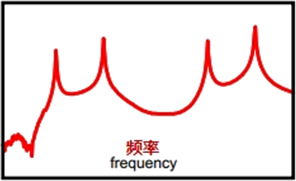
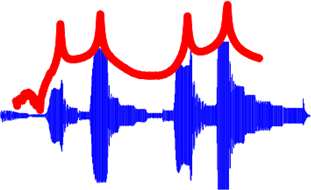
这个时域数据提供了非常有用的信息。但是如果采集到时域数据,并利用快速傅立叶变换将它变换到频域,则可以求得所谓的频响函数。现在有几点要关注:系统共振频率处,这个函数上有峰值。输入激励的振荡速率等于峰值频率的位置,观察到了时域最大响应。
现在如果将时域波形跟频响图形叠加在一起,会注意到时域波形达到最大值时的振荡频率与频响函数最大峰处的频率相一致。所以,既可以利用时域波形来确定幅值达到最大值处的频率,也可以用频响函数来确定固有频率何处发生。显然,用频响函数更容易求。
结构为何具有这些固有属性,你感到大为惊奇。对了,在这些固有频率处,变形形式也大为不同,依赖于激振力用哪个频率。
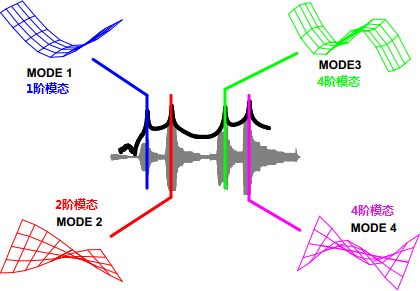
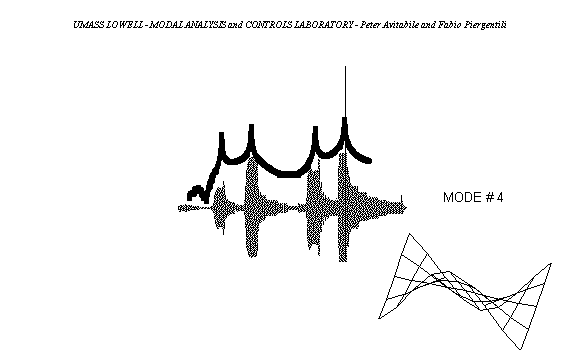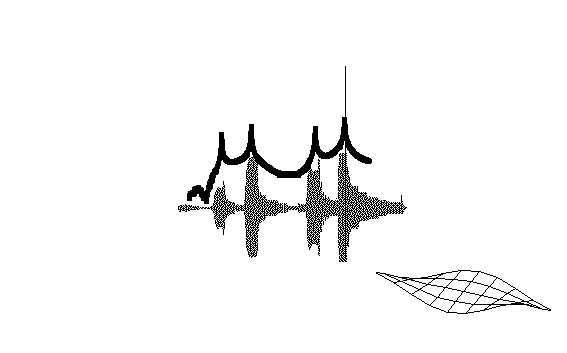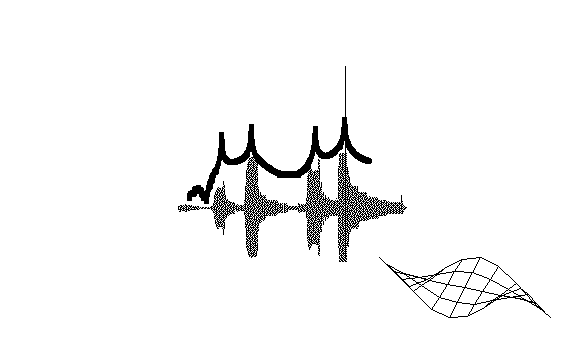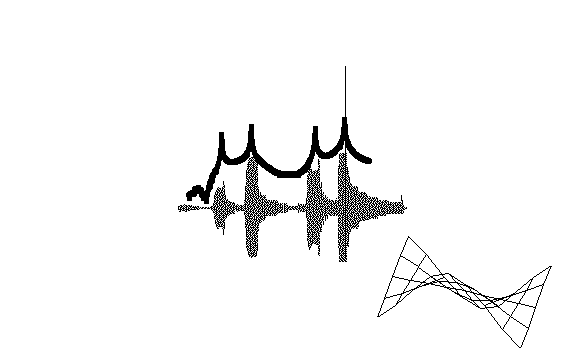
好了,我们来看一看,在每个固有频率处,结构上的变形形式是怎样的。在平板上均布45个加速度计,测量不同激振频率的平板响应幅值。如果在每个频率处驻留-每次一个固有频率-可以观察结构上的变形形式。图中显示了按某一阶系统固有频率激励时,得到的变形形式。在第一阶固有频率驻留时,平板具有第一阶弯曲变形形式,如蓝色所示。在第二阶固有频率驻留时,平板具有第一阶扭转变形形式,如红色所示。在第三、四阶固有频率驻留时,第二阶弯曲和第二阶扭转变形形式如绿色和紫红色所示。这些变形形式称为结构的模态振型。(从纯粹数学角度讲,这不完全正确。但事实上,此处简单讨论起见,这些变形形式非常接近于模态振型)
你看,我们设计的所有结构都具有这些固有频率和模态振型。从本质上讲,这些特性依赖于结构的质量和刚度,它决定了固有频率和模态振型何处存在。作为设计工程师,需要确定这些频率,并且需要知道当力激励结构时,它们是如何影响结构响应的。理解模态振型和受激结构如何振动,将有助于设计工程师设计出更优的结构。然而模态分析的内容很多,这只是一个非常简单的解释。
现在我们能够更好地理解模态分析是什么 — 它研究结构的固有特性。利用固有频率和模态振型(依赖于结构的质量和刚度分布)帮助设计噪声和振动方面应用的结构系统。我们利用模态分析来帮助设计所有类型的结构,包括汽车、飞机、航天器、计算机、网球拍、高尔夫球杆…等等。
我希望这个非常简明的介绍有助于解释模态分析是什么。我曾经利用上面的例子向我的妈妈解释模态分析,并且我认为她第一次真正了解我是从事什么工作的了。自此以后,听到妈妈给她的朋友们解释模态分析,使用了不少非常接近于模态分析的词,其中最接近的一次是她称之为面条分析(noodle analysis)…好了,有点扯远了!
![]()
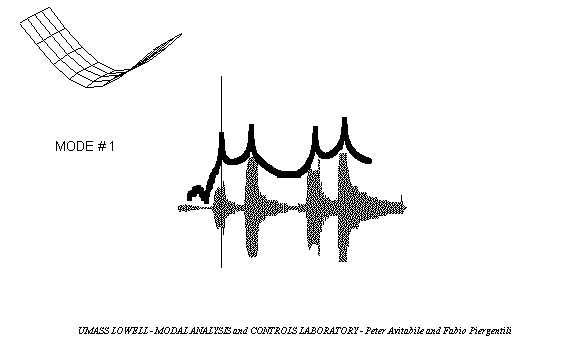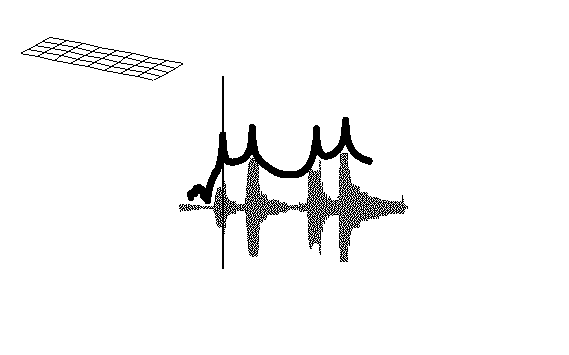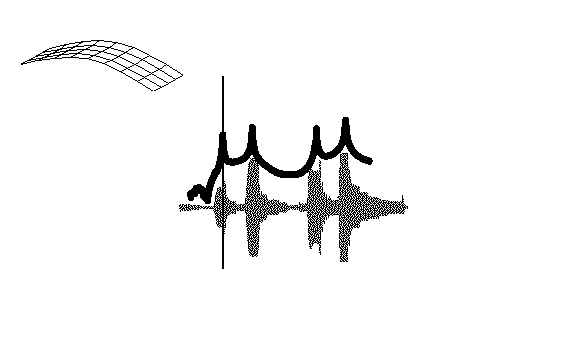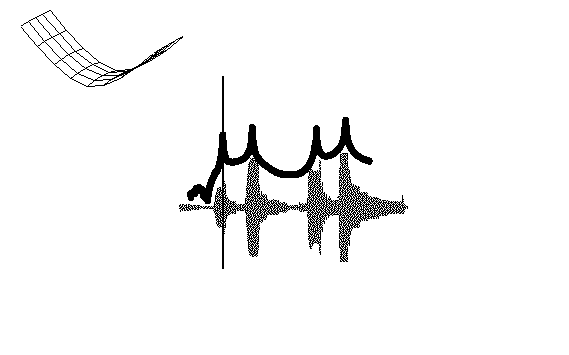
附 — 平板前四阶模态的振型动画:
![]()
下一篇:2.模态空间98.04—你能解释时域、频域和模态空间之间的差别吗?
![]()
扩展阅读[new]:
《振动:解析与试验模态分析》辛辛那提大学 Randall J. Allemang教授 (著) KSI科尚仪器 董书伟 (译)…
《振动:试验模态分析》辛辛那提大学 Randall J. Allemang教授 (著) KSI科尚仪器 董书伟 (译)…[new]