4. 频响函数推导

《振动：解析与试验模态分析》 辛辛那提大学 Randall J. Allemang教授 (著)，KSI科尚仪器 董书伟 (译)

4.1 理论

如果系统的解析模型早已存在，则前面讨论的所有技术都派得上用场。但从试验的角度来看，这种情况很少出现。通常，不借助于理论模型或者是为了验证理论模型，也必须解决实际系统或部分系统上的问题。

在本章先以频响函数测量结果作为基础，来定义真实结构的模态频率和阻尼值、模态向量、模态质量、模态刚度和模态阻尼。为完成这项任务，将要推导一个解析模型来表示结构上任意可测位置之间的传递函数。频响函数将与理论推导得到的传递函数直接相关。

从质量、刚度和阻尼矩阵的运动微分方程开始，建立无阻尼多自由度系统的传递函数表达式。

[M]\left \{ \ddot{x} \right \}+ [K] \left \{ x \right \} = \left \{f \right \} \qquad (4.1)

对式4.1进行拉氏变换，假设初始条件为零，则有：

\Big [ s^{2}[M] +[K] \Big ] \left \{ X(s) \right \} = \left \{F(s) \right \} \qquad (4.2)

令：

\big [ B(s) \big ] = \Big [ s^{2}[M] +[K] \Big ]

则式4.2变为：

\big [ B(s) \big ] \left \{ X(s) \right \} = \left \{ F(s) \right \} \qquad (4.3)

其中，称[B(s)]为系统阻抗矩阵或就称为系统矩阵。

式4.3左乘 [B(s)]^{-1} ，得到：

\big [ B(s) \big ]^{-1} \left \{ F(s) \right \} = \left \{ X(s) \right \}

定义：

\big [ H(s) \big ] = \big [ B(s) \big ]^{-1}

则：

\big [ H(s) \big ] \left \{ F(s) \right \} = \left \{ X(s) \right \} \qquad (4.4)

式4.4通过矩阵[H(s)]将系统响应\left \{X(s)\right \}与系统激励函数\left \{F(s) \right \} 联系起来。通常称矩阵[H(s)]为传递函数矩阵。

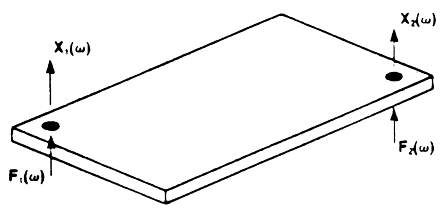
图4-1. 两输入-输出模型

针对一个两自由度系统，将式4.2-4.4展开，来详细查看系统矩阵中每个位置的元素。

\begin{bmatrix} M_{11} & M_{12} \\ M_{21} & M_{22} \end{bmatrix}\begin{Bmatrix} \ddot{x}_{1}\\ \ddot{x}_{2} \end{Bmatrix}+\begin{bmatrix} K_{11} & K_{12} \\ K_{21} & K_{22} \end{bmatrix} \begin{Bmatrix} x_{1}\\ x_{2} \end{Bmatrix}=\begin{Bmatrix} f_{1}\\ f_{2} \end{Bmatrix} \qquad (4.5)

对式4.5进行拉氏变换，得到：

\Bigg [ \begin{bmatrix} M_{11} &M_{12} \\ M_{21}&M_{22} \end{bmatrix}s^2 +\begin{bmatrix} K_{11} &K_{12} \\ K_{21} &K_{22} \end{bmatrix} \Bigg ]\begin{Bmatrix} X_{1}(s)\\ X_{2}(s) \end{Bmatrix}=\begin{Bmatrix} F_{1}(s)\\ F_{2}(s) \end{Bmatrix}

则，

\big [B(s) \big ] \left \{X(s) \right \} = \left \{ F(s) \right \}

其中：

定义传递函数为阻抗矩阵的逆矩阵：

\big [\, B(s) \, \big ]^{-1} = \big [\, H(s)\, \big]

对于这个解析的情况，阻抗矩阵的逆矩阵可以通过将阻抗矩阵的伴随矩阵除以阻抗矩阵的行列式求得，如下所示：

\big [\, B(s) \, \big ]^{-1} = \dfrac{\begin{bmatrix} M_{22}s^{2}+K_{22} & -(M_{12}s^{2}+K_{12}) \\ -(M_{21}s^{2}+K_{21}) & M_{11}s^{2}+K_{11} \end{bmatrix}}{(M_{11}s^{2}+K_{11})(M_{22}s^{2}+K_{22})-(M_{21}s^2+K_{21})(M_{12}s^2+K_{12})} \qquad (4.6)

注意，式4.6的分母是\left |B(s) \right |，它是系统的特征方程或称频率方程。这强调了如下事实：复模态频率(\lambda_{r})为系统的全局属性，因为这个特征方程出现在[\,H(s)\,]的每一项上。这个特征方程可以按照根的因子式乘积的形式表示，则：

\left | B(s) \right |= E\left ( s-\lambda_{1} \right ) \left ( s-\lambda_{2} \right ) \left ( s-\lambda_{3} \right ) \left ( s-\lambda_{4} \right )

其中：

则，接下来两自由度系统的式4.6可以写成：

\begin{Bmatrix} X_{1}(s) \\ X_{2}(s) \end{Bmatrix} = \dfrac{\begin{bmatrix} M_{22}s^{2}+K_{22} & -(M_{12}s^{2}+K_{12}) \\ -(M_{21}s^{2}+K_{21}) & M_{11}s^{2}+K_{11} \end{bmatrix}}{E\left ( s-\lambda_{1} \right ) \left ( s-\lambda_{2} \right ) \left ( s-\lambda_{3} \right ) \left ( s-\lambda_{4} \right )} \begin{Bmatrix} F_{1}(s) \\ F_{2}(s) \end{Bmatrix} \qquad (4.7)

传递函数矩阵[H(s)]可以定义为：

\big [\, H(s) \, \big ] = \begin{bmatrix} H _{11}(s) & H _{12}(s) \\ H _{21}(s) & H _{22}(s) \end{bmatrix}

其中，例如：

H_{11}(s) = \dfrac{M_{22}s^2+K_{22}}{E\left ( s-\lambda_{1} \right ) \left ( s-\lambda_{2} \right ) \left ( s-\lambda_{3} \right ) \left ( s-\lambda_{4} \right )} \qquad (4.8)

现在，式4.4可以表示为：

\begin{bmatrix} H _{11}(s) & H _{12}(s) \\ H _21{s} & H _{22}(s) \end{bmatrix}\begin{Bmatrix} F_{1}(s) \\ F_{2}(s) \end{Bmatrix} = \begin{Bmatrix} X _{1}(s) \\ X _{2}(s) \end{Bmatrix} \qquad (4.9)

式4.9乘出来，得到：

\begin{aligned} H _{11}(s)F _{1}(s) + H _{12}(s)F _{2}(s) &= X _{1}(s) \\ H _{21}(s)F _{1}(s) + H _{22}(s)F _{2}(s) &= X _{2}(s) \end{aligned} \qquad (4.10)

如果式4.10中F_{2}(s) = 0，则：

\begin{aligned} H _{11}(s)F _{1}(s) &= X _{1}(s) \\ H _{21}(s)F _{1}(s) &= X _{2}(s) \end{aligned}

这便得到了熟悉的传递函数关系式（输出比上输入）：

\begin{aligned} H _{11}(s) &= \dfrac{X _{1}(s)}{F _{1}(s)} \\ H _{21}(s) &= \dfrac{X _{2}(s)}{F _{1}(s)} \end{aligned}

通常

H _{pq}(s) = \dfrac{X _{p}(s)}{F _{q}(s)}

其中：

因此，利用一个固定输入（激振器系统），移动响应来测量[H]矩阵的一列，使用一个移动输入（力锤）和固定响应来测量一行。需要重申的是：下角标p，q不仅代表物理位置，同样也表示方向或方位。

因此，H_{11}(s)是通过F_{1}(s)激励系统，测量响应X_{1}(s)得到的传递函数。同样，H_{21}(s)是通过F_{1}(s)激励系统，测量响应X_{2}(s)得到的传递函数。类似地，可以让F_{1}(s)=0，通过F_{2}(s)激励系统，测量响应X_{1}(s)和X_{2}(s)得到H_{12}(s)和H_{22}(s)。

同单自由度的情况一样，称式4.8中的分母多项式为特征方程。注意式4.6中表示的所有传递函数都具有相同的分母多项式。这个分母多项式(特征方程)的根为系统的模态频率。

因为特征方程的系数为实数，那么特征根将以复共轭对的方式出现。记住这点，重写式4.8得到下面的结果：

H_{11}(s) = \dfrac{M_{22}s^2+K_{22}}{E\left ( s-\lambda_{1} \right ) \left ( s-\lambda_{1}^{*} \right ) \left ( s-\lambda_{2} \right ) \left ( s-\lambda_{2}^{*} \right )} \qquad (4.11)

其中，\lambda_{1}，\lambda_{1}^{*}，\lambda_{2}和\lambda_{2}^{*}为特征方程的根。也称特征方程的根为传递函数H_{11}(s)的极点。

4.2 解析模型 – 标量/矩阵多项式（多自由度）

式4.11或由质量，阻尼和刚度矩阵模型定义的任何传递函数的一般表达式可以改写为自变量s的分子多项式除以自变量s的分母多项式的形式。这两个多项式都包含系统质量、阻尼、刚度的离散值的不同数值组合的系数。分母多项式的根为系统模态频率，可看作系统的全局属性。分子多项式的根为系统零点，是系统的局部属性，依赖于传递函数的特定输入-输出关系。单个传递函数的通用多项式模型可以使用标量系数写成如下的形式：

\dfrac{X_{p}(s)}{F_{q}(s)} =H_{pq}(s)= \dfrac{\beta _{n}(s)^{n}+\beta _{n-1}(s)^{n-1}+\cdots+\beta _{1}(s)^{1}+\beta _{0}(s)^{0}}{\alpha_{m}(s)^{m}+\alpha_{m-1}(s)^{m-1}+\cdots+\alpha_{1}(s)^{1}+\alpha_{0}(s)^{0}} \qquad (4.12)

前面的模型可以写为更简洁的形式，如下所示：

\dfrac{X_{p}(s)}{F_{q}(s)} = \dfrac{\displaystyle\sum_{k=0}^{n}\beta_{k}(s)^{k}}{\displaystyle\sum_{k=0}^{m}\alpha_{k}(s)^{k}}

进一步整理得到如下的方程，它是含有未知\alpha项和\beta项的线性方程。

\displaystyle\sum_{k=0}^{m}\alpha_{k}(s)^{k}X_{p}(s)= \displaystyle\sum_{k=0}^{n}\beta_{k}(s)^{k}F_{q}(s) \qquad (4.13)

对这个模型进行推广来表示一般的多输入多输出情形，使用矩阵多项式形式，如下所示：

\displaystyle\sum_{k=0}^{m} \Big [ [\alpha_{k}](s)^{k} \Big ] \left \{X(s) \right\}= \displaystyle\sum_{k=0}^{n} \Big [ [\beta_{k}](s)^{k} \Big ] \left \{F(s) \right \} \qquad (4.14)

通过限定变量s(s=j\omega)并且进行一些矩阵运算，可以使用前面的模型来表示频响函数FRF。如果上面的方程两侧同时右乘激振力向量的厄米特（复共轭）转置(\left \{F(s) \right \}^{H})，得到如下方程：

\displaystyle\sum_{k=0}^{m} \Big [ [\alpha_{k}](s)^{k} \Big ] \left \{X(s) \right\} \left \{F(s) \right\}^{H}= \displaystyle\sum_{k=0}^{n} \Big [ [\beta_{k}](s)^{k} \Big ] \left \{F(s) \right \} \left \{F(s) \right\}^{H}

注意，在上面方程中，当s=j \omega时，向量积定义为互功率谱([G_{xf}(s)] = \left \{X(s) \right\} \left \{F(s) \right \}^{H})和自功率谱([G_{ff}(s)] = \left \{F(s) \right\} \left \{F(s) \right \}^{H})（经过平均）。

\displaystyle\sum_{k=0}^{m} \Big [ [\alpha_{k}](s)^{k} \Big ] \Big [G_{xf}(s) \Big ] =\displaystyle\sum_{k=0}^{n} \Big [ [\beta_{k}](s)^{k} \Big ] \Big [G_{ff}(s) \Big ]

上面的方程右乘自功率谱矩阵的逆矩阵：

\displaystyle\sum_{k=0}^{m} \Big [ [\alpha_{k}](s)^{k} \Big ] \Big [G_{xf}(s) \Big ] \Big [G_{ff}(s) \Big ]^{-1}=\displaystyle\sum_{k=0}^{n} \Big [ [\beta_{k}](s)^{k} \Big ] \Big [\,I \, \Big ]

最后，注意到，当s=j \omega时，对多输入多输出的情况，互谱矩阵与自谱逆矩阵的乘积([G_{xf}(s)][G_{ff}(s)]^{-1})为频响函数矩阵([H(s)])。上述方程可写成最终的形式：

\displaystyle\sum_{k=0}^{m} \Big [ [\alpha_{k}](j \omega)^{k} \Big ] \big [H(\omega) \big ]=\displaystyle\sum_{k=0}^{n} \Big [ [\beta_{k}](j \omega)^{k} \Big ] \Big [\,I \, \Big ] \qquad (4.15)

对单输入单输出的情况，上述方程为：

\displaystyle\sum_{k=0}^{m} \alpha_{k}(j \omega)^{k} H_{pq}(\omega) =\displaystyle\sum_{k=0}^{n} \beta_{k}(j \omega)^{k} \qquad (4.16)

4.3 解析模型 – 部分分式形式（留数）

式4.11通常按照其部分分式的形式展开进行表示。也即：

H_{11}(s) = \dfrac{X_{1}(s)}{F_{1}(s)} = \dfrac{c_{1}}{(s- \lambda_{1})}+\dfrac{c_{2}}{(s- \lambda_{1}^{*})}+\dfrac{c_{3}}{(s- \lambda_{2})}+\dfrac{c_{4}}{(s- \lambda_{2}^{*})} \qquad (4.17)

可以按照与单自由度情形中类似的方式，求得常数c_{1} \rightarrow c_{4}。让式4.11和式4.17相等，得到：

\dfrac{M_{22}s^2+K_{22}}{E\left ( s-\lambda_{1} \right ) \left ( s-\lambda_{1}^{*} \right ) \left ( s-\lambda_{2} \right ) \left ( s-\lambda_{2}^{*} \right )} = \dfrac{X_{1}(s)}{F_{1}(s)} = \dfrac{c_{1}}{(s- \lambda_{1})}+\dfrac{c_{2}}{(s- \lambda_{1}^{*})}+\dfrac{c_{3}}{(s- \lambda_{2})}+\dfrac{c_{4}}{(s- \lambda_{2}^{*})} \quad (4.18)

注意，式4.18乘以(s-\lambda_{1})，并求式子在s=\lambda_{1}时的值，可以得到c_{1}。所以：

c_{1} = \dfrac{M_{22}\lambda_{1}^{2}+K_{22}}{E \left ( \lambda_{1}-\lambda_{1}^{*} \right ) \left ( \lambda_{1}-\lambda_{2} \right ) \left ( \lambda_{1}-\lambda_{2}^{*} \right )} = A_{111} \qquad (4.19)

按照类似方式：

\begin{aligned} c_{2} &= \dfrac{M_{22}\lambda_{1}^{*2}+K_{22}}{E \left ( \lambda_{1}^{*}-\lambda_{1} \right ) \left ( \lambda_{1}^{*}-\lambda_{2} \right ) \left ( \lambda_{1}^{*}-\lambda_{2}^{*} \right )} = c_{1}^{*}= A_{111}^{*} \\ c_{3} &= \dfrac{M_{22}\lambda_{2}^{2}+K_{22}}{E \left ( \lambda_{2}-\lambda_{1} \right ) \left ( \lambda_{2}-\lambda_{1}^{*} \right ) \left ( \lambda_{2}-\lambda_{2}^{*} \right )} = A_{112} \\ c_{4} &= \dfrac{M_{22}\lambda_{2}^{*2}+K_{22}}{E \left ( \lambda_{2}^{*}-\lambda_{1} \right ) \left ( \lambda_{2}^{*}-\lambda_{1}^{*} \right ) \left ( \lambda_{2}^{*}-\lambda_{2} \right )} = c_{3}^{*}= A_{112}^{*} \end{aligned}

式4.17变为：

H_{11}(s) = \dfrac{A_{111}}{(s- \lambda_{1})}+\dfrac{A_{111}^{*}}{(s- \lambda_{1}^{*})}+\dfrac{A_{112}}{(s- \lambda_{2})}+\dfrac{A_{112}^{*}}{(s- \lambda_{2}^{*})} \qquad (4.20)

因此，一个两自由度系统的传递函数可以由两个单自由度系统的和表示（第2.5节）。这个结果现在可以外推到任意的自由度数目。

式4.20按照这种求和的形式可以重写为：

H_{11}(s) = \displaystyle \sum _{r=1}^{2} \Bigg[ \dfrac{A_{11r}}{s-\lambda_{r}}+\dfrac{A_{11r}^{*}}{s- \lambda_{r}^{*}} \Bigg ] \qquad (4.21)

跟在单自由度的情形一样，还是称A_{11r}为与极点\lambda_{r}相关的留数。

利用跟推导式4.21相同的推理方法，其他的系统传递函数可以表示为：

H_{21}(s) = \displaystyle \sum _{r=1}^{2} \Bigg[ \dfrac{A_{21r}}{s-\lambda_{r}}+\dfrac{A_{21r}^{*}}{s- \lambda_{r}^{*}} \Bigg ] \qquad (4.22)

H_{12}(s) = \displaystyle \sum _{r=1}^{2} \Bigg[ \dfrac{A_{12r}}{s-\lambda_{r}}+\dfrac{A_{12r}^{*}}{s- \lambda_{r}^{*}} \Bigg ] \qquad (4.23)

H_{22}(s) = \displaystyle \sum _{r=1}^{2} \Bigg[ \dfrac{A_{22r}}{s-\lambda_{r}}+\dfrac{A_{22r}^{*}}{s- \lambda_{r}^{*}} \Bigg ] \qquad (4.24)

根据上述的部分分式展开式，现在式4.9可写为：

\begin{Bmatrix} X_{1}(s)\\ \\ X_{2}(s) \end{Bmatrix} = \begin{bmatrix} \displaystyle \sum _{r=1}^{2} \bigg[ \dfrac{A_{11r}}{s-\lambda_{r}}+\dfrac{A_{11r}^{*}}{s- \lambda_{r}^{*}} \bigg] & \displaystyle \sum _{r=1}^{2} \bigg[ \dfrac{A_{12r}}{s-\lambda_{r}}+\dfrac{A_{12r}^{*}}{s- \lambda_{r}^{*}} \bigg] \\ \displaystyle \sum _{r=1}^{2} \bigg[ \dfrac{A_{21r}}{s-\lambda_{r}}+\dfrac{A_{21r}^{*}}{s- \lambda_{r}^{*}} \bigg] & \displaystyle \sum _{r=1}^{2} \bigg[ \dfrac{A_{22r}}{s-\lambda_{r}}+\dfrac{A_{22r}^{*}}{s- \lambda_{r}^{*}} \bigg] \end{bmatrix} \begin{Bmatrix} F_{1}(s) \\ \\ F_{2}(s) \end{Bmatrix} \;\; (4.25)

也可以将式4.21-4.24合在一起，按部分分式的形式将传递函数矩阵[H(s)]重写为：

\big [\,H(s)\,\big] = \dfrac{\begin{bmatrix} A_{111} & A_{121} \\ A_{211} & A_{221}\end{bmatrix}}{(s-\lambda_{1})} + \dfrac{\begin{bmatrix} A_{111}^{*} & A_{121}^{*} \\ A_{211}^{*} & A_{221}^{*} \end{bmatrix}}{(s-\lambda_{1}^{*})} +\dfrac{\begin{bmatrix} A_{112} & A_{122} \\ A_{212} & A_{222}\end{bmatrix}}{(s-\lambda_{2})} +\dfrac{\begin{bmatrix} A_{112}^{*} & A_{122}^{*} \\ A_{212}^{*} & A_{222}^{*}\end{bmatrix}}{(s-\lambda_{2}^{*})} \;(4.26)

上述方程每一项中的分子矩阵被称为留数矩阵。注意，每一个系统模态频率（极点）都有一个与之相关的单独矩阵。同样也注意到，与复共轭模态频率相关的留数矩阵也是复共轭的。

前面已经求得A_{111}（式4.19）。现在也可以按照同样的方式求得A_{211}，A_{121}，A_{221}。完成这些之后，可以求得极点\lambda_{1}的第1个留数矩阵的形式为：

A_{211} = \dfrac{-(M_{21} \lambda_{1}^{2}+K _{21})}{E(\lambda_{1}-\lambda_{1}^{*})(\lambda_{1}-\lambda_{2})(\lambda_{1}-\lambda_{2}^{*})}

A_{121} = \dfrac{-(M_{12} \lambda_{1}^{2}+K _{12})}{E(\lambda_{1}-\lambda_{1}^{*})(\lambda_{1}-\lambda_{2})(\lambda_{1}-\lambda_{2}^{*})}

A_{221} = \dfrac{-(M_{11} \lambda_{1}^{2}+K _{11})}{E(\lambda_{1}-\lambda_{1}^{*})(\lambda_{1}-\lambda_{2})(\lambda_{1}-\lambda_{2}^{*})}

式4.26右侧的第1项可以重新写成如下形式：

\dfrac{\begin{bmatrix} A_{111} &A_{121} \\A_{211} &A_{221} \end{bmatrix}}{(s-\lambda_{1})} = \dfrac{\begin{bmatrix} M_{22} \lambda _{1}^{2}+K_{22} & -(M_{12}\lambda_{1}^{2}+K_{12})\\ -(M_{21}\lambda_{1}^{2}+K_{21}) &M_{11}\lambda_{1}^{2}+K_{11} \end{bmatrix}}{E(\lambda_{1}-\lambda_{1}^{*})(\lambda_{1}-\lambda_{2})(\lambda_{1}-\lambda_{2}^{*})(s-\lambda_{1})} \quad (4.27)

注意，式4.27右侧的分子矩阵是第3.8节所讨论的系统矩阵的伴随矩阵。因此根据式3.41，得：

\begin{bmatrix} M_{22} \lambda _{1}^{2}+K_{22} & -(M_{12}\lambda_{1}^{2}+K_{12})\\ -(M_{21}\lambda_{1}^{2}+K_{21}) &M_{11}\lambda_{1}^{2}+K_{11} \end{bmatrix} = \gamma_{1} \begin{bmatrix} \psi_{1}\psi_{1} & \psi_{1}\psi_{2}\\ \psi_{2}\psi{1} & \psi_{2}\psi_{2}\end{bmatrix}_{1} \quad(4.28)

将式4.28代入到式4.27中，得到：

\dfrac{\begin{bmatrix} A_{111} &A_{121} \\A_{211} &A_{221} \end{bmatrix}}{(s-\lambda_{1})} = \dfrac{\gamma_{1} \begin{bmatrix} \psi_{1}\psi_{1} & \psi_{1}\psi_{2}\\ \psi_{2}\psi{1} & \psi_{2}\psi_{2}\end{bmatrix}_{1}}{E(\lambda_{1}-\lambda_{1}^{*})(\lambda_{1}-\lambda_{2})(\lambda_{1}-\lambda_{2}^{*})(s-\lambda_{1})} \quad (4.29)

最后，可以建立传递函数数据（通过留数矩阵）和系统模态向量之间的关系。式4.29表明留数矩阵与伴随矩阵具有相同的结构：每一列都包含着相同模态向量的一个冗余估计，仅仅相差一个常数。一般情况下这种关系按照下列方式表示：

对极点\lambda_{1}来说：

\begin{bmatrix} A_{111} & A_{121} \\ A_{211} & A_{221} \end{bmatrix} = Q_{1} \begin{bmatrix} \psi_{1}\psi_{1} & \psi_{1}\psi_{2} \\ \psi_{2} \psi_{1} & \psi_{2} \psi_{2} \end{bmatrix}_{1}

一般情况下，对极点\lambda_{r}：

\begin{bmatrix} A_{11r} & A_{12r} \\ A_{21r} & A_{22r} \end{bmatrix} = Q_{r}\begin{Bmatrix} \psi_{1} \\ \psi_{2}\end{Bmatrix}_{r} \begin{Bmatrix} \psi_{1} \\ \psi_{2}\end{Bmatrix}_{r}^{T} = Q_{r} \begin{bmatrix} \psi_{1}\psi_{1} & \psi_{1}\psi_{2} \\ \psi_{2} \psi_{1} & \psi_{2} \psi_{2} \end{bmatrix}_{r} \quad(4.30)

其中：

式4.30表明，关于留数矩阵，留数矩阵的每一行和每一列都包含着相同的模态向量，这个相同的模态向量与模态向量的一个元素以及归一化常数相乘。对于试验的情况来讲，这是非常重要的结果。因此，假设一行或一列内的所有留数不全是零，那么仅仅根据留数矩阵的一行或一列就可以估计出模态向量。这将完全确定那个特定极点的模态向量。根据试验要求，为了估计留数矩阵中的某个元素，必须测量频响函数。在某个行或列的每个元素都不是零的假设条件下，只需要N次而不是N \times N次测量即可。只要测得这些信息后，就可以合成得到留数矩阵中的所有其他项。

前面的讨论代表了测量的最低要求。为了确保不丢失模态向量或者为了利用不同行或列的冗余信息，通常要测量更多的行或列。

应该指出，式4.30中的比例常数Q_{r}是不唯一的，因为这个常数取决于模态向量如何归一的选择。这与模态向量表示自由度之间的相对运动这个概念是一致的。然而，要注意，留数是带有尺度的量，依赖于频响函数的单位。

4.4 模态向量示例

前面使用过的两自由度系统的传递函数矩阵现在用来确定模态向量。

将质量和刚度值代入式4.6，得到：

\begin{aligned} \big[ H(s) \big ] &= \dfrac{\begin{bmatrix} (10s^{2}+6) & 2 \\ 2 & (5s^{2}+4) \end{bmatrix}}{(5s^{2}+4)(10s^2+6)-(-2)(-2)} \\ \big[ H(s) \big ] &= \dfrac{\begin{bmatrix} (10s^{2}+6) & 2 \\ 2 & (5s^{2}+4) \end{bmatrix}}{50(s^{4}+7/5 s^{2}+2/5)} \end{aligned}

前面已经计算得到特征方程的根为：

\begin{aligned} \lambda_{1} &= j \sqrt{2/5} \;(rad/sec) \qquad \lambda_{1}^{*} = -j \sqrt{2/5} \; (rad/sec) \\ \lambda_{2} &= j \;(rad/sec) \qquad \qquad \;\; \lambda_{2}^{*} = -j\; (rad/sec) \end{aligned}

则：

\big[ H(s) \big ] = \dfrac{\begin{bmatrix} (10s^{2}+6) & 2 \\ 2 & (5s^{2}+4) \end{bmatrix}}{50(s-j \sqrt{2/5})(s+j \sqrt{2/5})(s-j)(s+j)}

现在传递函数H_{11}(s)可以按照部分分式展开式的形式表示：

\begin{aligned} H_{11}(s) &= \dfrac{10s^2+6}{50(s-j \sqrt{2/5})(s+j \sqrt{2/5})(s-j)(s+j)} \\ H_{11}(s) &= \dfrac{A_{111}}{(s-j \sqrt{2/5})} + \dfrac{A_{111}^{*}}{(s+j \sqrt{2/5})} +\dfrac{A_{112}}{(s-j)}+\dfrac{A_{112}^{*}}{(s+j)} \end{aligned}

\begin{aligned} A_{111} &= - \dfrac{j \sqrt{2/5}}{12} \qquad A_{111}^{*} = \dfrac{j \sqrt{2/5}}{12} \\ A_{112} &= - \dfrac{j}{15} \qquad \qquad A_{112}^{*} = \dfrac{j }{15} \end{aligned}

按照相同方式，也可以确定余下的传递函数的其他留数。

现在，系统传递函数矩阵[H(s)]可以按照部分分式表示为：

\big [\, H(s) \, \big]= \dfrac{\begin{bmatrix} -\dfrac{j \sqrt{2/5}}{12} & -\dfrac{j \sqrt{2/5}}{12} \\ -\dfrac{j \sqrt{2/5}}{12} & -\dfrac{j \sqrt{2/5}}{12} \end{bmatrix}}{\left ( s-j\sqrt{2/5} \right )} + \dfrac{\begin{bmatrix} \dfrac{j \sqrt{2/5}}{12} & \dfrac{j \sqrt{2/5}}{12} \\ \dfrac{j \sqrt{2/5}}{12} & \dfrac{j \sqrt{2/5}}{12} \end{bmatrix}}{\left ( s+j\sqrt{2/5} \right )}

+ \dfrac{\begin{bmatrix} \dfrac{-j }{15} & \dfrac{j}{30} \\ \dfrac{j }{30} & \dfrac{-j}{60} \end{bmatrix}}{\left ( s-j \right )} +\dfrac{\begin{bmatrix} \dfrac{j }{15} & \dfrac{-j}{30} \\ \dfrac{-j }{30} & \dfrac{j}{60} \end{bmatrix}}{\left ( s+j \right )}

记住，与极点\lambda_{1}相关的模态向量跟极点\lambda_{1}的留数矩阵成比例。注意，前两个留数矩阵恰是互为共轭的。因此，极点\lambda_{1}^{*}的模态向量恰是极点\lambda_{1}的模态向量的共轭。后面的两个留数矩阵也是如此。对于极点的共轭对，情况总是如此。

极点\lambda_{1} = \sqrt{2/5}的模态向量可以从第一个留数矩阵中提取出来。

利用式4.29和4.30，第一个极点的模态向量可以与留数矩阵联系起来。

Q_{1}\left\{ \psi \right \}_{1} \left \{ \psi \right \}_{1}^{T} = Q_{1} \begin{bmatrix} \psi_{1}\psi_{1} & \psi_{1} \psi_{2} \\ \psi_{2}\psi_{1} & \psi_{2}\psi_{2} \end{bmatrix}_{1}

Q_{1}\left\{ \psi \right \}_{1} \left \{ \psi \right \}_{1}^{T} = \begin{bmatrix} -\dfrac{j \sqrt{2/5}}{12} & -\dfrac{j \sqrt{2/5}}{12} \\ -\dfrac{j \sqrt{2/5}}{12} & -\dfrac{j \sqrt{2/5}}{12} \end{bmatrix}_{1}

现在，可以将常数Q_{1} = \pm \dfrac{j \sqrt{2/5}}{12}作为因子项从留数矩阵中提取出来。这时候这个常数的选择是完全任意的，这是由于模态向量的绝对幅值是完全任意的。

\begin{bmatrix} \psi_{1}\psi_{1} & \psi_{1} \psi_{2} \\ \psi_{2}\psi_{1} & \psi_{2}\psi_{2} \end{bmatrix}_{1} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}_{1}

因此，第1阶模态的模态向量为：

\begin{Bmatrix} \psi_{1} \\ \psi_{2} \end{Bmatrix}_{1} = \begin{Bmatrix} 1 \\ 1 \end{Bmatrix}_{1}

类似地，第2阶模态的模态向量为：

Q_{2}\left\{ \psi \right \}_{2} \left \{ \psi \right \}_{2}^{T} = Q_{2} \begin{bmatrix} \psi_{1}\psi_{2} & \psi_{1} \psi_{2} \\ \psi_{2}\psi_{1} & \psi_{2}\psi_{2} \end{bmatrix}_{2} = \begin{bmatrix} \dfrac{-j}{15} & \dfrac{j}{30}\\ \dfrac{j}{30} & \dfrac{-j}{60} \end{bmatrix}_{2}

现在跟前面一样，按照相同的任意方式，可以将Q_{2} = \pm \dfrac{-j}{60}作为因子项从留数矩阵中提取出来。

\begin{bmatrix} \psi_{1}\psi_{1} & \psi_{1} \psi_{2} \\ \psi_{2}\psi_{1} & \psi_{2}\psi_{2} \end{bmatrix}_{2} = \begin{bmatrix} 4 & -2 \\ -2 & 1 \end{bmatrix}_{2}

让两个矩阵的各元素相等，得到：

\begin{aligned} \psi_{1}\psi_{1} &= \psi_{1}^{2} = 4 \qquad \psi_{1}=2 \\ \psi_{2}\psi_{1} &= -2 \qquad \quad \;\;\, \psi_{2}=-1 \end{aligned}

因此：

\begin{Bmatrix} \psi_{1} \\ \psi_{2} \end{Bmatrix}_{2} = \begin{Bmatrix} 2 \\ -1 \end{Bmatrix}_{2}

直接使用留数矩阵的任意一行或列作为模态向量，可以直接得到这两个模态向量。

4.5 解析模型 – 通用部分分式模型（留数）

回想两自由度系统的式4.21：

H_{11}(s) = \displaystyle \sum _{r=1}^{2} \dfrac{A_{11r}}{(s-\lambda_{r})}+\dfrac{A_{11r}^{*}}{(s- \lambda_{r}^{*})}

现在，将式4.21推广到N自由度系统，如下所示：

H_{11}(s) = \displaystyle \sum _{r=1}^{N} \dfrac{A_{11r}}{(s-\lambda_{r})}+\dfrac{A_{11r}^{*}}{(s- \lambda_{r}^{*})} \qquad (4.31)

\Big [\, H_{pq}(s) \, \Big ] = \displaystyle \sum _{r=1}^{N} \dfrac{\big [A_{pqr} \big ]}{(s-\lambda_{r})}+\dfrac{\big [A_{pqr}^{*} \big]}{(s- \lambda_{r}^{*})} \qquad (4.32)

进一步，整个系统传递函数[\,H(s)\,]可以推广为：

\Big [\, H(s) \, \Big ] = \displaystyle \sum _{r=1}^{N} \dfrac{\big [\,A\,\big ]_{r}}{(s-\lambda_{r})}+\dfrac{\big [\, A ^{*} \, \big]_{r}}{(s- \lambda_{r}^{*})} \qquad (4.33)

直接按照系统的模态向量，得：

\Big [\, H(s) \, \Big ] = \displaystyle \sum _{r=1}^{N} \dfrac{Q_{r}\left \{ \psi \right \}_{r}\left \{ \psi \right \}_{r}^{T}}{(s-\lambda_{r})}+\dfrac{Q_{r}^{*}\left \{ \psi \right \}_{r}^{*}\left \{ \psi \right \}_{r}^{*T}}{(s- \lambda_{r}^{*})} \qquad (4.34)

式3.34是系统传递函数矩阵的一般形式。如后面所示，当考虑有阻尼系统时，这个形式也不改变。记住，不过，完整的传递函数是不能测的。一而再说，实际上我们测取的是频响函数，它刚好是取式4.34在s=j\omega时的值。

4.6 留数与模态向量的关系

在4.3节中建立的留数矩阵和模态向量之间的关系可以按照更为正式或严格的方式进行推导。这里有一点非常重要：在试验情况下，模态向量和模态归一（模态质量）之间关系的关键在于前面章节中所定义的留数。接下来的讨论目前将限定于无阻尼和/或比例阻尼的情形。将在后面的章节中讨论一般阻尼情形下的关系。

留数矩阵和模态向量之间关系的推导与推导留数矩阵和系统伴随矩阵之间关系（3.8节）的相同办法进行。先定义阻抗矩阵为：

[B(s)] = \big[ [M]s^2+[C]s+[K] \big] \qquad (4.35)

其中：

根据矩阵代数：

[B(s)][B(s)]^{-1} = [\,I\,] \qquad (4.36)

注意，阻抗矩阵的逆矩阵为传递函数矩阵，得：

[B(s)][H(s)] = [\,I\,] \qquad (4.37)

根据式4.33，将传递函数矩阵替换为等效的部分分式模型，得：

\big [\, I \, \big ] = \displaystyle \sum _{r=1}^{N} \dfrac{[B(s)] [A ]_{r}}{(s-\lambda_{r})}+\dfrac{[B(s)] [ A ^{*} ]_{r}}{(s- \lambda_{r}^{*})} \qquad (4.38)

对任意某阶模态r，上式中的每一项乘以(s=\lambda_{r})，并计算等式在s=\lambda_{r}时的值（除了与\lambda_{r}相关的项之外，其他的所有项都消掉了）：

\big [ \, 0\, \big ] = \Big [\,B(\lambda_{r}) \, \Big] \big [\,A\,\big]_{r} \qquad(4.39)

注意，上式证明了留数矩阵[A]_{r}的每一列必然跟与\lambda_{r}相关的模态向量成比例，就如同在伴随矩阵中的情形一样（第3.8节）。类似的，留数矩阵的结构必然跟伴随矩阵的结构相同。

[A]_{r} = Q_{r}\left\{ \psi \right \} \left \{\psi \right \}_{r}^{T} \qquad (4.40)

\big [\, A \, \big ]_{r} = Q _{r}\begin{bmatrix} \psi_{1}\psi_{1} &\psi_{1}\psi_{2} & \;\cdot \; & \;\cdot \; & \;\cdot \; & \;\cdot \; & \psi_{1}\psi_{N} \\ \psi_{2}\psi_{1} &\psi_{2}\psi_{2} & \;\cdot \; & \;\cdot \; & \;\cdot \; & \;\cdot \; & \psi_{2}\psi_{N} \\ \;\cdot \; &\;\cdot \; & \;\cdot \; & \;\cdot \; & \;\cdot \; & \;\cdot \; & \cdot \; \\ \;\cdot \; &\;\cdot \; & \;\cdot \; & \;\cdot \; & \;\cdot \; & \;\cdot \; & \cdot \; \\ \psi_{N}\psi_{1} &\psi_{N}\psi_{2} & \;\cdot \; & \;\cdot \; & \;\cdot \; & \;\cdot \; & \psi_{N}\psi_{N} \end{bmatrix}_{r}

其中：

4.7 留数与模态质量的关系

对于比例阻尼的情形，包含齐次的无阻尼情形，也可以建立留数与模态质量之间的关系，它跟从质量矩阵中按解析方式求得的模态质量是一致的。从式4.38和4.40开始：

\big [\, I \, \big ] = \displaystyle \sum _{r=1}^{N}\dfrac{ [B(s)] Q_{r}\left \{ \psi \right \}_{r}\left \{ \psi \right \}_{r}^{T}}{(s-\lambda_{r})}+\dfrac{[B(s)]Q_{r}^{*}\left \{ \psi ^{*} \right \}_{r} \left \{ \psi^{*} \right \}_{r}^{T}}{(s- \lambda_{r}^{*})} \qquad (4.41)

注意，对于比例阻尼系统，模态向量总是实（正则）模态。则模态向量的共轭与模态向量相同(\left\{\psi\right\}_{r} = \left\{\psi^{*}\right\}_{r})。进行此替换并且式4.41两边同时左乘\left\{\psi\right\}_{t}^{T}：

\left\{\psi\right\}_{t}^{T} = \displaystyle \sum _{r=1}^{N} \dfrac{\left\{\psi\right\}_{t}^{T}[B(s)]Q_{r}\left \{ \psi \right \}_{r}\left \{ \psi \right \}_{r}^{T}}{(s-\lambda_{r})}+\dfrac{\left\{\psi\right\}_{t}^{T}[B(s)]Q_{r}^{*}\left \{ \psi \right \}_{r} \left \{ \psi \right \}_{r}^{T}}{(s- \lambda_{r}^{*})} \qquad (4.42)

将式4.35代入式4.42：

\left\{\psi\right\}_{t}^{T} = \displaystyle \sum _{r=1}^{N} \dfrac{Q_{r}\left\{\psi\right\}_{t}^{T}\Big [[M]s^{2}+[C]s+[K]\Big]\left \{ \psi \right \}_{r}\left \{ \psi \right \}_{r}^{T}}{(s-\lambda_{r})}+ \qquad \qquad

\qquad \qquad\dfrac{Q_{r}^{*} \left\{\psi\right\}_{t}^{T}\Big [[M]s^{2}+[C]s+[K]\Big]\left \{ \psi \right \}_{r} \left \{ \psi \right \}_{r}^{T}}{(s- \lambda_{r}^{*})} \qquad (4.43)

应用模态向量与质量、阻尼和刚度矩阵之间的正交特性，除了保留与模态t相关的项之外，消去所有其他项：

\left\{\psi\right\}_{t}^{T} = \dfrac{Q_{t}\big (M_{t}\,s^{2}+C_{t}\,s+K_{t}\big)\left \{ \psi \right \}_{t}^{T}}{(s-\lambda_{t})}+ \dfrac{Q_{t}^{*} \big (M_{t}\,s^{2}+C_{t}\,s+K_{t}\big) \left \{ \psi \right \}_{t}^{T}}{(s- \lambda_{t}^{*})} \qquad (4.44)

从式4.41的各项中消去\left \{\psi\right\}_{t}^{T}，得到下面的标量等式：

1 = \dfrac{Q_{t}\big (M_{t}\,s^{2}+C_{t}\,s+K_{t}\big)}{(s-\lambda_{t})}+ \dfrac{Q_{t}^{*} \big (M_{t}\,s^{2}+C_{t}\,s+K_{t}\big) }{(s- \lambda_{t}^{*})} \quad (4.45)

从上式中，去掉分式形式：

(s-\lambda_{t})(s-\lambda_{t}^{*})=Q_{t}\big (M_{t}\,s^{2}+C_{t}\,s+K_{t}\big)(s-\lambda_{t}^{*})+ Q_{t}^{*} \big (M_{t}\,s^{2}+C_{t}\,s+K_{t}\big) (s- \lambda_{t}) \quad (4.46)

注意，根据定义：

\big (M_{t}\,s^{2}+C_{t}\,s+K_{t}\big)=M_{t}(s-\lambda_{t})(s-\lambda_{t}^{*}) \qquad (4.47)

将式4.47代入式4.46，并消去等式两侧的通项(s-\lambda_{t})(s-\lambda_{t}^{*})：

1=Q_{t}M_{t}(s-\lambda_{t}^{*})+Q_{t}^{*}M_{t}(s-\lambda_{t}) \qquad (4.48)

计算当s=\lambda_{t}时式4.49的值，得到最后的关系式：

\begin{aligned} 1&=Q_{t}M_{t}(\lambda_{t}-\lambda_{t}^{*}) \qquad (4.49) \\ 1&=Q_{t}M_{t}(2j\omega_{t}) \quad \, \qquad (4.50) \\ M_{t}&=\dfrac{1}{2j\omega_{t}Q_{t}} \qquad \qquad \quad (4.51)\end{aligned}

式4.51表示模态质量、归一化与留数、模型向量之间的关系（回想式4.40）。那么，当求得模态t的留数信息并且选定了模态t的某种模态向量归一化形式之后，就可以确定归一化常数Q_{t}。则式4.51可用于确定模态t的模态质量，它与模态向量归一化相一致。这意味着只要模态向量选择的一致，则不同方法之间的模态质量就可以进行比较了（例如，解析与试验之间）。

上一章 第3章 多自由度系统 – 振动：解析与试验模态分析

下一章 第5章 一般阻尼系统 – 振动：解析与试验模态分析

返回《振动：解析与试验模态分析》中文翻译目录

扩展阅读[new]：
《模态空间系列文章》Peter Avitabile教授(著) KSI科尚仪器 董书伟 (译)…

《振动：试验模态分析》辛辛那提大学Randall J. Allemang教授(著) KSI科尚仪器 董书伟(译)…[new]