8.模态空间99.04 — 我还是不理解曲线拟合… 你是怎样从FRFs中得到模态振型的？

MODAL SPACE – IN OUR OWN LITTLE WORLD

模态空间 – 在我们自己的小世界中     Pete Avitabile(著) KSI科尚仪器 董书伟（译）

我还是不理解曲线拟合… 你是怎样从FRFs中得到模态振型的？

嗯…那我们看看能否澄清这个问题。

到目前为止，对大多数人来讲，模态参数估计（通常称为曲线拟合）可能是试验模态分析中最难以理解的部分。我知道我可以写出所有的公式来解释这点。但是，我可能会烦死你。我不但必须要写出关于模态参数估计过程的所有公式，而且我也必须指出这些公式建立了留数与模态振型之间的关系。另一方面，留数当然是另一个抽象的概念。（哎呀，我多么希望，人们以前就称它为模态振型，而不是留数，因为，这只会搞得大家一头雾水。）

上次（1999年2月），我们曾经讨论了曲线拟合模型，以及用于估计参数的基本公式，其中一种形式表示如下

\left [ H\left ( s \right ) \right ]= lower \; residuals \,+\,\displaystyle\sum_{k=i}^{j}\dfrac{\left [ A_{k} \right ]}{\left ( s-s_k \right )} +\dfrac{\left [ A_{k}^* \right ]}{\left ( s-s_{k}^* \right )}\,+\,upper \;residuals
现在，矩阵[A]中的那些项是留数，是从曲线拟合过程中得到的；我们同时从公式的分母中得到极点，或频率和阻尼。现在，这些留数可以证明与模态振型有关。不必深入到每一步，我们可以得到如下的关系式（将某些项展开）
\left [ A\left ( s \right ) \right ]_{k}=q_{k}\left \{ u_{k} \right \}\left \{ u_{k} \right \}^T
\large \begin{bmatrix} a_{11k} &a_{12k} &a_{13k} &\cdots \\ a_{21k} &a_{22k} &a_{23k} &\cdots \\ a_{31k}&a_{32k} &a_{33k} &\cdots \\ \vdots &\vdots &\vdots &\ddots \end{bmatrix}=q_{k}\begin{bmatrix} u_{1k}u_{1k} &u_{1k}u_{2k} &u_{1k}u_{3k} &\cdots \\ u_{2k}u_{1k} &u_{2k}u_{2k} &u_{2k}u_{3k} &\cdots \\ u_{3k}u_{1k} &u_{3k}u_{2k} &u_{3k}u_{3k} &\cdots \\ \vdots &\vdots &\vdots &\ddots \end{bmatrix}
好了，如果我们来观察矩阵的每一列元素，可以看出列元素中包含模态振型，带有某些标量乘数；我们同时也可以看出，因为互易性，各行也包含模态振型。如果我们观察某一列，例如第1列，那么，我们可以看到
\begin{Bmatrix} a_{11k}\\ a_{21k}\\ a_{31k}\\ \vdots \end{Bmatrix}=q_{k}u_{1k}\begin{Bmatrix} u_{1k}\\ u_{2k}\\ u_{3k}\\ \vdots \end{Bmatrix}
因此，留数无非是模态振型乘以一个标量因数 — 模态振型在参考点位置的数值u，同时乘以归一常数q。（归一常数q允许模态振型可以用不同的归一常数来表示（单位模态质量，单位长度，等。）

太好了，这样，可能有些公式你能完全理解或领会，也可能不能完全理解或领会。或许解释这个概念的更好办法是借助于一些简单的图形。让我们回过头来看看先前时候讨论过的那个简单平板（1998年1月），同时，也很简单地来解释我们是如何从测量结果中得到模态振型的（这样，你或许可以领会数学可以为我们做什么？）。

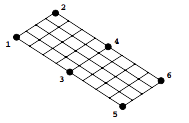
现在，我们在平板上进行测量，这样我们共得到6个FRFs — 在4个角以及2个中点位置。从这些测量结果中，我们希望能够确定前两阶模态看起来是什么样子。现在，我们可以观察FRFs的对数幅值，但这不是很有用，因为在这个图上，所有的峰都将是正的。

FRF的虚部是一个包含更多信息的图形。这不但显示了幅值，而且，更重要的是，显示了响应的方向。不去深入研究全部专业的数学内由，我们知道，FRF的虚部的峰值幅度与留数直接相关（同时，留数与模态振型相关）。这个近似公式如下所示

h\left ( j \omega \right )|_{ \omega \rightarrow \omega_{n} }=\dfrac{a_1}{\left ( j \omega_{n}+\sigma-j \omega_{d} \right )}+\dfrac{a_{1}^{*}}{\left ( j \omega_{n}+\sigma+j \omega_{d} \right )}
a_{1}=\sigma h\left ( j \omega \right )|_{\omega \rightarrow \omega_{n}}
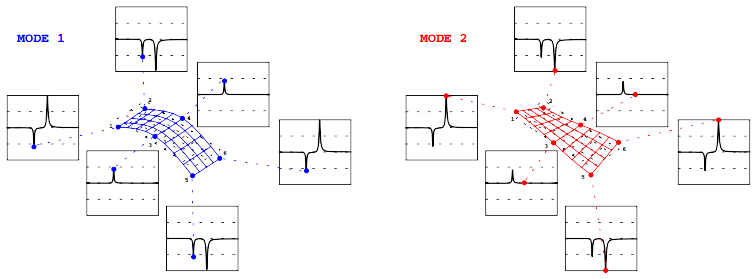
通常称这个非常简单的确定模态振型的方法为峰值拾取法，因为我们拾取了FRF的峰值。现在，针对每个测点位置的各个测量结果，我们观察某些峰值。（在所示的所有图形中，幅值的刻度范围从-1到+1，并且短划线是1/2。另外，去掉了频率轴。）现在我们首先主要研究1阶模态，然后再考察2阶模2。

观察1阶模态的测点1的FRF。注意到，这个幅值是0.5，并且是负的。如果我们观察测点2，则我们看到幅值也是0.5，并且也是负的。这意味着，对1阶模态，测点1和测点2按照相同的幅度、相同的方向运动。如果我们观察测点5和测点6，我们可以看到跟测点1和测点2相同的情况。这样一来，我们可以看出测点1、2、5、和6都是按照相同的幅度，相同的方向运动。

此处，要说明的非常重要的一点是，如果我仅仅测量这4个点，那么在我看来，平板的模态振型将是刚体模态（所有4个点按照相同的幅度一起运动）。用于描述系统模态振型的测点太少时，这是个常见的问题。

现在，对于1阶模态来讲，观察测点3。注意到，因为幅值是0.5，且是正的。那么，测点4也是如此这般。因此，我们看到，测点3和测点4具有相同的幅度，并且按照相同的方向一起运动。但是我们也注意到，测点3和测点4是按照与其他测点的相反的方向运动的。现在，尽管我们测量的点不超过6个，但我们开始看到了平板正在变形成一种形式，一种平板弯曲的特征形式。如果我们测量了更多的点，那么我们将会看到一个更加明确的模态振型。

现在，如果我们观察2阶模态，我们可以一步一步来考察，并且观察所有测点，这样，我们将看到的是，测点1和2具有相同的幅度，但是现在它们按相反的方向运动。对于测点5和6，情况也是如此。但是，我们注意到，测点1和5也是按照相反的方向运动；测点2和6同样如此。这样，我们看出，对于模态2，存在某种扭曲或扭转类型的变形形式。如果我们观察测点3和4，我们注意到，这些点具有零值。这是因为测点3和4是平板扭转模态的节点。同样，添加更多点可以更好地确定振型。

所以现在我们可以看出，对于每阶模态的峰值，FRF虚部的峰值与平板模态振型直接相关。不必深细所有的数学内在根由，留数是从曲线拟合过程中提取出来的因项，并且这些留数与平板的模态振型直接相关。为使情况简单起见，已经按照图形方式说明了这一点。

我希望，这个解释有助于澄清关于我们是如何从FRFs中得到模态振型的这个谜团。好好思考一下这个问题，如果你有关于模态分析的如何其他问题，问我好了。

上一篇：7. 模态空间99.02 — 曲线拟合搞得我一头雾水，所有这些不同的技术是什么意思？

下一篇：9. 模态空间99.06 — 工作变形和模态振型之间有什么差别？

返回模态空间中文翻译目录

扩展阅读[new]：
《振动：解析与试验模态分析》辛辛那提大学Randall J. Allemang教授(著) KSI科尚仪器 董书伟(译)…