5. 一般阻尼系统

《振动：解析与试验模态分析》 辛辛那提大学 Randall J. Allemang教授 (著)，KSI科尚仪器 董书伟 (译)

5.1 非比例阻尼系统

实际上，物理结构或系统通常是由很多按不同方式连接在一起的子结构构成。这些子结构可以由不同的材料制作而成，如，金属、塑料或木材。此外，这些子结构通过铆钉、螺栓、螺钉、阻尼器、弹簧、焊接、摩擦等方式相互之间联接起来。同时，结构的空间几何形状也可能非常复杂，如汽车排气系统。所有这些因素都影响结构的固有动态特性。对这些结构来说，系统的质量、阻尼和刚度分布（矩阵）更为复杂。通常，对于实际结构，此般系统的阻尼矩阵并不总是跟系统质量和/或刚度矩阵成比例。因此，这类系统的阻尼归类为非比例阻尼。

从解析的意义看，这种一般类型的阻尼系统的模态分析不能用前面所讨论的无阻尼系统特征值问题的公式来描述。记住，在解析的意义上，模态分析的目的是找到一个坐标变换将原始运动方程组解耦。可以证明，这个坐标变换是一个由系统模态向量所组成的矩阵。这些模态向量可以根据那个系统的特征值问题的解来确定。对于无阻尼或比例阻尼系统，这个坐标变换将系统刚度、阻尼和刚度矩阵对角化。当系统包含非比例阻尼时，前面用到的特征值问题的公式化方法将不能得到把系统的运动方程组解耦的模态向量（特征向量）。化解这个问题的方法首先见于Duncan和Collar发表的文献，这种方法是将一个N自由度系统的原始运动方程组重构整合为等价的2N一阶微分方程组，称为哈密顿正则方程。可以按照之前已经讨论过的类似办法对这个方程组进行求解。

对于非比例阻尼，前面所讨论的坐标变换可以将系统的质量和刚度矩阵对角化，但不能将系统的阻尼矩阵对角化。因此，当一个系统存在非比例阻尼时，在N维物理空间建立的运动方程组是耦合在一起的。幸运的是，在2N维状态空间建立的运动方程组则可以解耦。这是通过借助一个N维恒等矩阵来扩大原始的N维物理空间方程实现的，如下所示。

假设一个粘性、非比例阻尼系统可以由式5.1来表示：

\left [ M \right ]\left \{ \ddot{x} \right \}+\left [ C \right ]\left \{ \dot{x} \right \}+\left [ K \right ]\left \{ x \right \}=\left \{ f \right \} \qquad (5.1)

通过式5.2所示的恒等式可以将这个系统方程扩大：

\left [ M \right ]\left \{ \dot{x} \right \}-\left [ M \right ]\left \{ \dot{x} \right \}=\left \{ 0 \right \} \qquad (5.2)

式5.1和5.2按照下面的方式组合在一起，得到一个含有2N个方程的新系统。注意，式5.3中的所有矩阵都是对称的，并且现在式5.3具有经典的特征值解的形式。式5.3所用的符号与很多数学和/或控制论教材中的符号一致。

[A]\left\{\dot{y}\right\}+[B]\left\{y\right\} = \left\{ f' \right \} \qquad (5.3)

其中：

由式5.3构建齐次方程，有：

[A]\left\{\dot{y}\right\}+[B]\left\{y\right\} = \left\{ 0 \right \} \qquad (5.4)

解式5.4得到这个扩大的2N方程系统的复数固有频率（特征值）和复数模态向量（特征向量）。注意，按照这种数学形式，可以直接得到特征值（不是特征值的平方），并且2N个特征向量的长度是2N。从这个2N方程系统的特征向量矩阵（状态空间模态矩阵）可以看到特征向量的准确形式。注意，2N方程系统的特征向量用符号\phi表示，而原始的N方程系统的特征向量用符号\psi表示。

现在，这个非比例阻尼系统的状态空间模态矩阵[\phi]可以组合在一起。

\big [ \phi \big ]=\begin{bmatrix} \left \{ \phi \right \}_{1} & \left \{ \phi \right \}_{2} & \left \{ \phi \right \}_{3} & \cdots & \left \{ \phi \right \}_{r} & \cdots & \left \{ \phi \right \}_{2N} \end{bmatrix} \qquad (5.5a)

根据用于式5.3中的坐标变换，特征向量矩阵的每一列（每个特征向量）是由想要得到的模态向量及位于其上的导数构成。这个结构如式5.5b所示。

\big [ \phi \big ]=\begin{bmatrix} \lambda_{1}\left \{ \psi \right \}_{1} & \lambda_{2}\left \{ \psi \right \}_{2} & \lambda_{3}\left \{ \psi \right \}_{3} & \cdots & \lambda_{r}\left \{ \psi \right \}_{r} & \cdots & \lambda_{2N}\left \{ \psi \right \}_{2N} \\ \;\;\,\;\left \{ \psi \right \}_{1} & \;\,\;\;\left \{ \psi \right \}_{2} & \;\;\;\;\left \{ \psi \right \}_{3} & \cdots &\;\;\; \;\left \{ \psi \right \}_{r} & \cdots & \;\;\; \;\;\;\;\left \{ \psi \right \}_{2N} \end{bmatrix} \qquad (5.5b)

5.1.1 特征向量的加权正交性

与无阻尼系统情况的类似，系统矩阵[A]和[B]的加权正交关系成立。

\left\{\phi \right\}_{r}^{T}[A]\left\{\phi\right\}_{s} = \textbf{0} \qquad(5.6)
\left\{\phi\right \}_{r}^{T}[B]\left\{\phi\right\}_{s} = \textbf{0} \qquad(5.7)

现在术语模态A和模态B可按如下方式定义。注意，这些量具有跟无阻尼和比例阻尼情况下的模态质量、模态刚度相同的特性。

\left\{\phi \right\}_{r}^{T}[A]\left\{\phi\right\}_{r} = M_{A_{r}} \qquad(5.8)
\left\{\phi \right\}_{r}^{T}[B]\left\{\phi\right\}_{r} = M_{B_{r}} \qquad(5.9)

术语模态A和模态B是非比例阻尼情况下的模态归一因子，它们就像模态质量、模态刚度可以作为无阻尼和比例阻尼情况下的模态归一因子那样。只要复模态向量存在，就应该用模态A和模态B进行模态归一。注意，即使对于无阻尼和比例阻尼情况，也可以用模态A和模态B进行模态归一。

注意，特征向量矩阵（状态空间模态矩阵）提供了一个坐标变换，它将物理状态空间坐标系统转化为解耦的主状态空间坐标系统。

[A]\left\{\dot{y}\right\}+[B]\left\{y\right\} = \left\{ f' \right \} \qquad (5.10)

[A] \big[\phi \big] \left\{\dot{q}\right\}+[B] \big[\phi \big] \left\{q\right\} = \left\{ f' \right \} \qquad (5.11)

\big[\phi \big]^{T} [A] \big[\phi \big] \left\{\dot{q}\right\}+\big[\phi \big]^{T} [B] \big[\phi \big] \left\{q\right\} = \big[\phi \big]^{T} \left\{ f' \right \} \qquad (5.12)

对第r阶特征值/特征向量：

M_{A_{r}}\dot{q}_{r}+M_{B_{r}}=f'_{r} \qquad(5.13)

这个解耦的方程有下面形式的特征方程：

M_{A_{r}}\,s +M_{B_{r}}=0 \qquad(5.14)

这意味这对于每一阶模态，模态A和模态B具有如下的关系：

M_{A_{r}}\,\lambda_{r} +M_{B_{r}}=0 \qquad(5.15)

M_{A_{r}}\,\lambda_{r} =-M_{B_{r}} \qquad(5.16)

在这里将不再进一步深入讲解这个概念，感兴趣的读者可以参考由Tse，Morse和Hinkle编写的《机械振动》第6章，或者由Leonard\; Meirovitch编写的《振动解析方法》第9章。

从试验的角度看，非比例阻尼系统的问题解决办法跟无阻尼或比例阻尼系统的解决办法相同。无论结构具有什么类型的阻尼，比例阻尼抑或非比例阻尼，都可以测得系统的频响函数。由此，可以根据频响函数测量结果确定留数，利用留数求得系统模态向量。尽管方法跟之前一样，但对于具有非比例阻尼的系统，模态向量的结果将多少有点复杂。作为非比例阻尼情形导致差别的示例，将再次使用之前例子中用过的同一个两自由度系统，不同的是将不再使阻尼矩阵与质量和/或刚度矩阵成比例。

5.2 比例阻尼系统

对于可以用比例阻尼概念从数学上表示的这类物理阻尼机制，前面已经讨论过，针对无阻尼情况下的可以将系统质量矩阵和刚度矩阵对角化的坐标变换，同样也可以将系统阻尼矩阵对角化。因此，当一个系统存在比例阻尼时，跟之前一样，耦合的运动方程系统可以转换为一个方程系统，这个方程系统代表一个易于求解的单自由度系统的解耦系统。实现这点的过程如下：

假设一个粘性阻尼系统可以由式5.17表示：

[M]\left\{\ddot{x}\right\}+[C]\left\{\dot{x}\right\}+[K]\left\{x\right\} = \left\{f\right\} \qquad(5.17)

作为理解这个问题的第一步是先求解无阻尼系统的特征值问题。

[M]\left\{\ddot{x}\right\}+[K]\left\{x\right\} = \left\{0\right\}

可以得到系统的固有频率（特征值）和模态向量（特征向量）。

现在，这个无阻尼系统的模态矩阵[\psi] 可以组合在一起。

\big[\psi\big] = \begin{bmatrix} \left\{\psi\right\}_{1} & \left \{ \psi \right \}_{2} & \cdots & \left \{ \psi \right \}_{N} \end{bmatrix}

现在，对式5.10进行坐标变换：

[x] = \big[\psi\big]\left\{q\right\}

[M]\big[\psi\big]\left\{\ddot{q}\right\}+[C]\big[\psi\big]\left\{\dot{q}\right\}+[K]\big[\psi\big]\left\{q\right\} = \left\{f\right\} \quad(5.18)

式5.18左乘[\psi]^{T}。

\big[\psi\big]^{T}[M]\big[\psi\big]\left\{\ddot{q}\right\}+\big[\psi\big]^{T}[C]\big[\psi\big]\left\{\dot{q}\right\}+\big[\psi\big]^{T}[K]\big[\psi\big]\left\{q\right\} = \big[\psi\big]^{T}\left\{f\right\} \quad(5.19)

由于模态向量的正交特性：

\big[\psi\big]^{T}[M]\big[\psi\big]=\left \lceil M \right \rfloor

\big[\psi\big]^{T}[K]\big[\psi\big]=\left \lceil K \right \rfloor

因为假设阻尼矩阵与质量和/或刚度矩阵成比例，阻尼矩阵也同样可以对角化。

[C]=\alpha [K] + \beta [K]

应用正交条件，得到：

\big[\psi\big]^{T} [C]\big[\psi\big]=\big[\psi\big]^{T} \left\{\alpha [M] + \beta [K] \right\} \big[\psi\big]

\big[\psi\big]^{T} [C]\big[\psi\big]=\alpha \big[\psi\big]^{T}[M]\big[\psi\big] + \beta \big[\psi\big]^{T}[K]\big[\psi\big]

\big[\psi\big]^{T} [C]\big[\psi\big]=\alpha \left \lceil M \right \rfloor + \beta \left \lceil K \right \rfloor

因此：

\big[\psi\big]^{T} [C]\big[\psi\big]= \left \lceil C \right \rfloor

其中：

因此，式5.19变为：

\left \lceil M \right \rfloor \left\{\ddot{q}\right\}+\left \lceil C \right \rfloor \left\{\dot{q}\right\}+\left \lceil K \right \rfloor \left\{q\right\} = \big [\psi\big]^{T} \left\{f(t)\right\} \quad (5.20)

式5.20表示一组解耦的阻尼单自由度系统。式5.20的第r个方程为：

M_{r}\ddot{q}_{r}+C_{r}\dot{q}+K_{r}q_{r} = f_{r}'(t) \qquad (5.21)

式5.21是下图所示系统的运动方程。

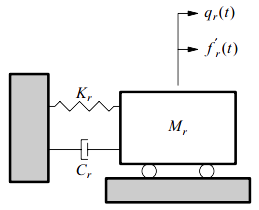
图5-1. 比例阻尼单自由度系统等效模型

这个阻尼单自由度系统的解在前面已经讨论过了。

5.3 比例阻尼示例

为了理解比例阻尼的概念，可以再次使用前面用过的无阻尼情况下的相同的两自由度例子。

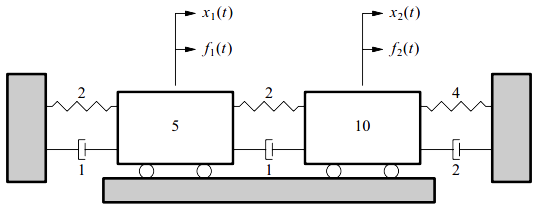
图5.2 含比例阻尼的两自由度模型

\begin{bmatrix} 5 & 0 \\ 0 & 10 \end{bmatrix} \begin{Bmatrix} \ddot{x}_{1} \\ \ddot{x}_{2} \end{Bmatrix} +\begin{bmatrix} 2 & -1 \\ -1 & 3 \end{bmatrix} \begin{Bmatrix} \dot{x}_{1} \\ \dot{x}_{2} \end{Bmatrix} +\begin{bmatrix} 4 & -2 \\ -2 & 6 \end{bmatrix} \begin{Bmatrix} x_{1} \\ x_{2} \end{Bmatrix} = \begin{Bmatrix} f_{1} \\ f_{2} \end{Bmatrix}

注意，阻尼矩阵[C]与刚度矩阵[K]成比例：

[C] = (\dfrac{1}{2})[K]

尽管这个阻尼矩阵的形式非常简单，但是最终的解却可以得出一个普遍特性，普适于所有可以由比例阻尼描述的问题。

利用之前算得的无阻尼系统的模态向量和固有频率，可以进行坐标变换：

\left\{x\right\} = \big[\psi\big] \left\{q\right\}

注意到，前面在3.6节中的例子的结果早就已经展示了运动方程对质量矩阵和刚度矩阵的解耦。因此，对于阻尼矩阵：

\begin{aligned} \big[\psi \big]^{T}[C]\big[\psi\big]&=\begin{bmatrix} \sqrt{1/15} & \sqrt{1/15} \\ \sqrt{2/15} & -\dfrac{1}{2}\sqrt{2/15}\end{bmatrix} \begin{bmatrix} 2 & -1 \\ -1 & 3 \end{bmatrix} \begin{bmatrix} \sqrt{1/15} & \sqrt{2/15} \\ \sqrt{1/15} & -\dfrac{1}{2}\sqrt{2/15}\end{bmatrix} \\ \big[\psi \big]^{T}[C]\big[\psi\big]&=\begin{bmatrix} 1/5 & 0 \\ 0 & 1/2 \end{bmatrix} \end{aligned}

根据模态坐标，这个变换后的系统将是：

\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{Bmatrix} \ddot{q}_{1} \\ \ddot{q}_{2} \end{Bmatrix} +\begin{bmatrix} 1/5 & 0 \\ 0 & 1/2 \end{bmatrix} \begin{Bmatrix} \dot{q}_{1} \\ \dot{q}_{2} \end{Bmatrix} +\begin{bmatrix} 2/5 & 0 \\ 0 & 1 \end{bmatrix} \begin{Bmatrix} q_{1} \\ q_{2} \end{Bmatrix} = \begin{Bmatrix} f_{1}'(t) \\ f_{2}'(t) \end{Bmatrix}

或如图所示：

图5-3. 比例阻尼多自由度等效模型

5.3.1 频响函数含义

可以从传递函数的角度通过确定模态频率和模态向量来求解这个相同的问题。系统的传递函数矩阵为：

\big[H(s)\big] = \dfrac{\begin{bmatrix} (M_{22}s^{2}+C_{22}s+K_{22}) & -(M_{12}s^2+C_{12}s+K_{12})\\ -(M_{21}s^{2}+C_{21}s+K_{21})& (M_{11}s^{2}+C_{11}s+K_{11})\end{bmatrix}}{\left | B(s) \right |} \quad(5.22)

\begin{aligned} \left | B(s) \right | = (& M_{11}s^{2}+C_{11}s+K_{11})(M_{22}s^2+C_{22}s+K_{22})\\&-(M_{21}s^{2}+C_{21}s+K_{21})(M_{12}s^{2}+C_{12}s+K_{12}) \end{aligned}

代入例子中的质量、阻尼和刚度矩阵的数值：

\big[H(s)\big] = \dfrac{\begin{bmatrix} (10s^{2}+3s+6) & (s+2)\\ (s+2)& (5s^{2}+2s+4)\end{bmatrix}}{50s^4+35s^3+75s^2+20s+20}

特征方程的根为：

\begin{aligned} \lambda_{1} & = -\dfrac{1}{10}+j \dfrac{\sqrt{39}}{10}\,(rad/sec) \qquad \lambda_{1}^{*} = -\dfrac{1}{10}-j \dfrac{\sqrt{39}}{10}\,(rad/sec)\\ \lambda_{2} & = -\dfrac{1}{4}+j \dfrac{\sqrt{15}}{4}\,(rad/sec) \qquad \;\, \lambda_{2}^{*} = -\dfrac{1}{4}-j \dfrac{\sqrt{15}}{4}\,(rad/sec) \end{aligned}

注意，现在阻尼系统的极点含有实部。前面（第2章）已经定义过传递函数的极点为：

\lambda_{r} = \sigma_{r}+j\omega_{r}

其中：

记住，在前面的无阻尼情况下，极点可以写为如下的形式：

\lambda_{r} = j\omega_{r}

其中：

假设行或列的所有元素不都等于零，那么仅仅利用最少的传递函数数据就可以确定系统模态向量。如果这是真的，那么可以利用系统传递函数矩阵的一行或一列来求出模态向量。例如，选择H_{11}(s)和H_{21}(s)，它是第一列。

首先，按照部分分式形式将H_{11}(s)和H_{21}(s)展开：

H_{11}(s) = \dfrac{10s^2+3s+6}{50(s-\lambda_{1})(s-\lambda_{1}^{*})(s-\lambda_{2})(s-\lambda_{2}^{*})}

经过一些运算后：

\begin{aligned} H_{11}(s) &= \dfrac{-j\dfrac{\sqrt{39}}{117}}{(s-\lambda_{1})} + \dfrac{j\dfrac{\sqrt{39}}{117}}{(s-\lambda_{1}^{*})} +\dfrac{-j\dfrac{4\sqrt{15}}{225}}{(s-\lambda_{2})} +\dfrac{j\dfrac{4\sqrt{15}}{225}}{(s-\lambda_{2}^{*})} \\ H_{21}(s) &= \dfrac{s+2}{50(s-\lambda_{1})(s-\lambda_{1}^{*})(s-\lambda_{2})(s-\lambda_{2}^{*})} \\ H_{21}(s) &= \dfrac{-j\dfrac{\sqrt{39}}{117}}{(s-\lambda_{1})} + \dfrac{j\dfrac{\sqrt{39}}{117}}{(s-\lambda_{1}^{*})} +\dfrac{-j\dfrac{2\sqrt{15}}{225}}{(s-\lambda_{2})} +\dfrac{j\dfrac{2\sqrt{15}}{225}}{(s-\lambda_{2}^{*})} \end{aligned}

回想，已经证明留数与模态向量成比例。因为仅使用了传递函数矩阵的一列，那么对每个模态频率也只能算得留数矩阵的一列。

因此，通过观察第一个极点\lambda_{1}对应的留数，可以得到模态向量为：

\begin{Bmatrix} \psi_{1} \\ \psi_{2} \end{Bmatrix}_{1} \rightarrow \begin{Bmatrix} \dfrac{-j\sqrt{39}}{117} \\ \dfrac{-j\sqrt{39}}{117} \end{Bmatrix}_{1} = \begin{Bmatrix} 1 \\ 1 \end{Bmatrix}_{1} \qquad(5.23)

对模态频率\lambda_{2}，模态向量结果为：

\begin{Bmatrix} \psi_{1} \\ \psi_{2} \end{Bmatrix}_{2} \rightarrow \begin{Bmatrix} \dfrac{-j4\sqrt{15}}{225} \\ \dfrac{j2\sqrt{15}}{225} \end{Bmatrix}_{2} = \begin{Bmatrix} 1 \\ -1/2 \end{Bmatrix}_{2} \qquad(5.24)

因此，根据这个比例阻尼系统的传递函数矩阵计算出来的模态向量与无阻尼系统是相同的。只要所考虑的系统含有比例阻尼，情况总是这样。

注意，研究的无阻尼和比例阻尼系统，不仅它们的模态向量是相同的，而且经过归一化后，模态向量乃是实数。对于实际系统，情况可能并非如此。因为模态向量为实数，通常称之为实模态或正则模态。

5.3.2 脉冲响应函数注意事项

现在可以讨论比例阻尼多自由系统的脉冲响应函数。记住，脉冲响应函数是传递函数的时域等价形式。一旦将多自由度系统的脉冲响应函数用公式表达出来之后，它就可以跟之前的单自由度系统进行比较。重写式4.24：

H_{pq}(s) = \displaystyle\sum_{r=1}^{N} \dfrac{A_{pqr}}{(s-\lambda_{r})} + \dfrac{A_{pqr}^{*}}{(s-\lambda_{r}^{*})} \qquad (5.25)

回想H_{pq}(s)的定义：

H_{pq}(s) = \dfrac{X_{p}(s)}{F_{q}(s)}

因此：

X_{p}(s) = F_{q}(s)\displaystyle\sum_{r=1}^{N} \dfrac{A_{pqr}}{(s-\lambda_{r})} + \dfrac{A_{pqr}^{*}}{(s-\lambda_{r}^{*})} \qquad (5.26)

如果用于激励自由度(q)的力为脉冲，那么其拉氏变换为单位值1。尽管是用这个概念来定义脉冲响应函数，一旦传递函数得到后，并且认为系统是线性，那么这类假设具有普遍性。

F_{q}(s)=1

因此自由度p处的系统脉冲响应函数为式5.19的拉氏逆变换：

h_{pq}(t) = \textbf{L}^{-1}\biggl\{X_{p}(s)\biggr\} = \textbf{L}^{-1}\biggl\{\displaystyle\sum_{r=1}^{N} \dfrac{A_{pqr}}{(s-\lambda_{r})} + \dfrac{A_{pqr}^{*}}{(s-\lambda_{r}^{*})}\biggr\} \qquad (5.27)

如果p=q，那么这将是驱动点脉冲响应函数。简单起见，可以将式5.27推广到两自由度情况(N=2)。

X_{p}(s)=\dfrac{A_{pp1}}{(s-\lambda_{1})}+\dfrac{A_{pp1}^{*}}{(s-\lambda_{1}^{*})}+\dfrac{A_{pp2}}{(s-\lambda_{2})}+\dfrac{A_{pp2}^{*}}{(s-\lambda_{2}^{*})} \quad(5.28)

h_{pp}(t) = \textbf{L}^{-1}\biggl\{X_{p}(s)\biggr\} = A_{pp1}\,e^{\lambda_{1}t} + A_{pp1}^{*}\,e^{\lambda_{1}^{*}t}+ A_{pp2}\,e^{\lambda_{2}t}+ A_{pp2}^{*}\,e^{\lambda_{2}^{*}t} \quad (5.29)

上文提到：

\begin{aligned} \lambda_{r} &= \sigma_{r}+j \omega_{r} \\ \lambda_{r}^{*} &= \sigma_{r}-j \omega_{r} \end{aligned}

同样，因为系统是比例阻尼的，留数皆为纯虚数。因此，下面的定义可以任意确定。这个定义将使后面公式中的三角恒等式更加显而易见。

\begin{aligned} A_{pp1} &= \dfrac{R_{pp1}}{2j} \\ A_{pp2} &= \dfrac{R_{pp2}}{2j} \end{aligned}

利用欧拉公式，式5.22接下来变为：

\begin{aligned} h_{pp}(t) = \dfrac{R_{pp1}}{2j}\Big( & e^{(\sigma_{1}+j \omega_{1})t} - e^{(\sigma_{1}-j \omega_{1})t} \Big) \\ & + \dfrac{R_{pp2}}{2j}\Big(e^{(\sigma_{2}+j \omega_{2})t} - e^{(\sigma_{2}-j \omega_{2})t} \Big) \end{aligned}

h_{pp}(t) = R_{pp1}\,e^{\sigma_{1}t}\dfrac{(e^{j\omega_{1}}-e^{-j\omega_{1}})}{2j}+R_{pp2}\,e^{\sigma_{2}t}\dfrac{(e^{j\omega_{2}}-e^{-j\omega_{2}})}{2j}

最后：

h_{pp}(t) = R_{pp1}\,e^{\sigma_{1}t} \sin(\omega_{1}t)+R_{pp2}\,e^{\sigma_{2}t}\sin(\omega_{2}t) \qquad(5.30)

将这个式子与前面得出的单自由度例子进行比较，注意到，这个脉冲响应函数不过是两个单自由度响应之和。另外也注意到，脉冲响应函数的幅值与两个模态向量的留数直接相关。这意味着，脉冲响应函数幅值与这两阶模态的模态向量直接相关，因为已经证明留数与模态向量成正比。

综上，一个传递函数，故而频响函数，可以表示为单自由度系统之和（式4.24）。一个典型的频响函数按照其实部和虚部如图5-4所示。这个频响函数H_{12}(\omega)表示在自由度2对系统施加激励引起的自由度1位置的系统响应。图5-5是图5-4的等价的脉冲响应函数。类似的，这个脉冲响应函数h_{12}(t)表示在自由度2对系统施加单位脉冲激励引起的自由度1位置的系统响应。注意，脉冲响应函数从t=0时为零开始，对于具有实模态的系统，这是应该的。因为传递函数是单自由度系统之和，每个单自由度系统的频响函数可以单独画出，如图5-6和5-8所示。注意，通过将图5-6和5-8加在一起，可以得到跟图5-4相同的图形。在图5-6和5-8中，虚部在实部过零点处为峰，在图5-4中，这并不十分准确。同样，每个单自由度系统的脉冲响应函数可以单独画出，如图5-7和5-9所示。这两个图求和与图5-5是相同的。因此，一个两自由度系统的脉冲响应函数就是2个阻尼衰减曲线之和。

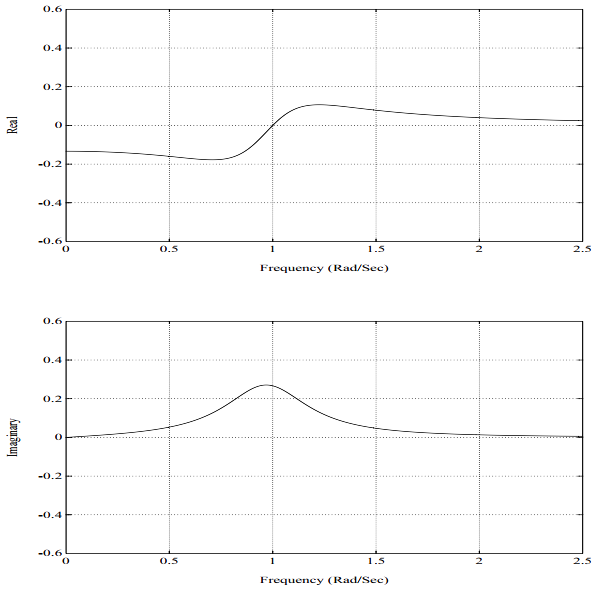
图5-4. 频响函数，2自由度系统，比例阻尼

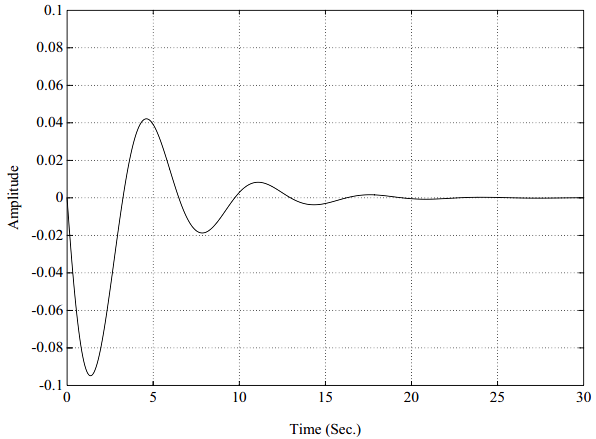
图5-5. 脉冲响应函数，2自由度系统，比例阻尼

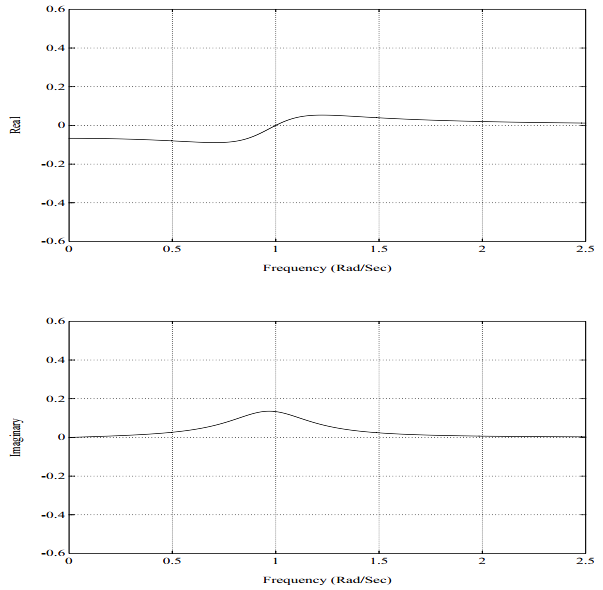
图5-6. 频响函数，2自由度系统，比例阻尼，第1阶模态

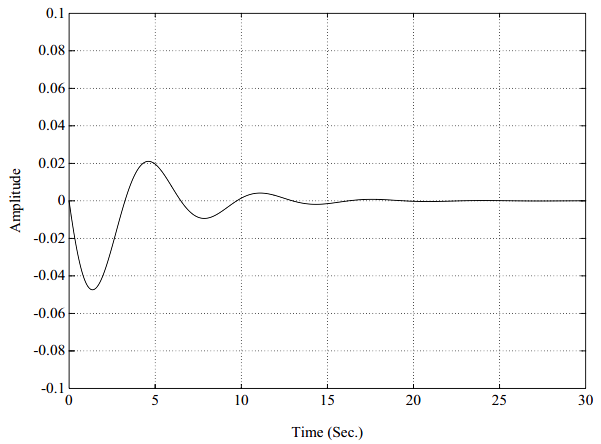
图5-7. 脉冲响应函数，2自由度系统，比例阻尼，第1阶模态

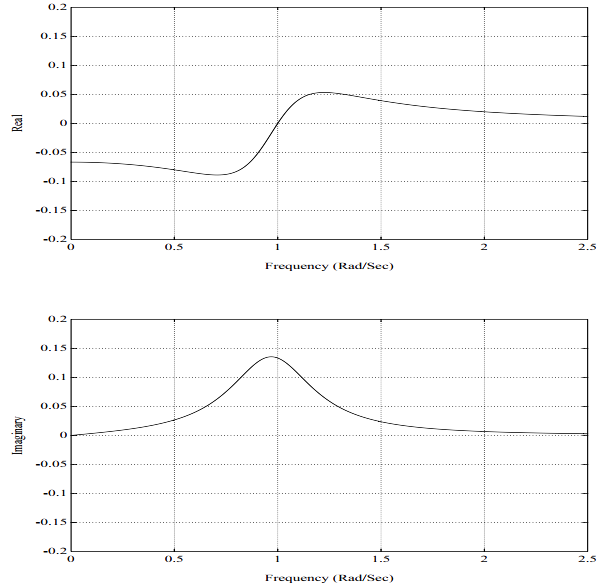
图5-8. 频响函数，2自由度系统，比例阻尼，第2阶模态

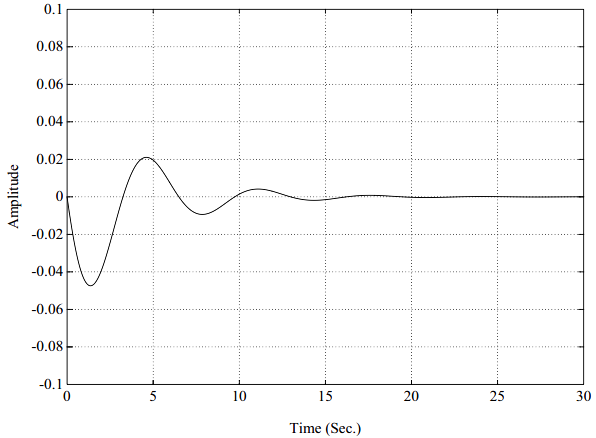
图5-9. 脉冲响应函数，2自由度系统，比例阻尼，第2阶模态

5.4 非比例阻尼示例

以前用过的质量、刚度相同的两自由度系统，现在将用来解释非比例阻尼的影响。

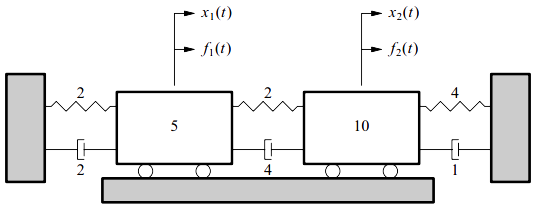
图5-10. 两自由度系统

选择阻尼系数，使其与质量和/或刚度不成比例。利用式5.22，所得系统的传递函数为：

\big[H(s)\big] = \dfrac{\begin{bmatrix} 10s^2+5s+6 & 4s+2 \\ 42+2 & 5s^2+6s+2 \end{bmatrix}}{50[s^4+(17/10)s^3+(42/25)s^2+(4/5)s+2/5]} \quad (5.31)

传递函数的极点为特征方程的根：

s^4+\dfrac{17}{10}s^3+\dfrac{42}{25}s^2+\dfrac{4}{5}s+\dfrac{2}{5}=0 \quad (5.32)

这些根为：

\begin{aligned} \lambda_{1} &= -0.095363+j0.629494 \,(rad/sec) \\ \lambda_{1}^{*} &= -0.095363-j0.629494 \,(rad/sec) \end{aligned}

\begin{aligned} \lambda_{2} &= -0.754635+j0.645996 \,(rad/sec) \\ \lambda_{2}^{*} &= -0.754635-j0.645996 \,(rad/sec) \end{aligned}

这些极点为系统的两阶振动模态的阻尼和频率参数。上文提到：\lambda_{r}=\sigma_{r}+j \omega_{r}。

跟之前一样，通过求解部分分式形式的传递函数矩阵的值可以确定系统模态向量。在前面的例子中，利用传递函数矩阵的第一列来确定模态向量。为了说明模态向量对于[H(s)]的所有元素的普遍性，这次将利用传递函数矩阵的最后一行。即：

H_{21}(s)和H_{22}(s)

通过在质量1处激励系统，测量质量2处的响应，测得H_{21}(s)）。同样，在质量2处激励系统，测量质量2处的响应，测得H_{22}(s)。现在将H_{22}(s)和H_{21}(s)按部分分式的形式展开。

H_{22}(s) = \dfrac{5s^2+6s+4}{50(s-\lambda_{1})(s-\lambda_{1}^{*})(s-\lambda_{2})(s-\lambda_{2}^{*})}

经过一些计算后：

\begin{aligned} H_{22}(s) = & \dfrac{0.003707-j 0.058760}{(s-\lambda_{1})}+\dfrac{0.003707+j 0.058760}{(s-\lambda_{1}^{*})} \\ &+ \dfrac{-0.003702-j 0.016358}{(s-\lambda_{2})}+\dfrac{-0.003702+j 0.016358}{(s-\lambda_{2}^{*})} \end{aligned}

同样：

H_{21}(s) = \dfrac{4s^2+2}{50(s-\lambda_{1})(s-\lambda_{1}^{*})(s-\lambda_{2})(s-\lambda_{2}^{*})}

经过一些计算后：

\begin{aligned} H_{21}(s) = & \dfrac{-0.003473-j 0.050100}{(s-\lambda_{1})}+\dfrac{-0.003473+j 0.050100}{(s-\lambda_{1}^{*})} \\ &+ \dfrac{0.003473+j 0.045270}{(s-\lambda_{2})}+\dfrac{0.003473-j 0.045280}{(s-\lambda_{2}^{*})} \end{aligned}

直接利用留数作为模态向量（不做任何正则化或归一化），可以得到下面的向量：

模态1： \lambda_{1} = -0.095363+j0.629494

\begin{Bmatrix} \psi_{1} \\ \psi_{2}\end{Bmatrix}_{1} = \begin{Bmatrix} -0.003473-j0.050100 \\ +0.003707-j0.058760 \end{Bmatrix}_{1}

模态2： \lambda_{1} = -0.754635+j0.645996

\begin{Bmatrix} \psi_{1} \\ \psi_{2}\end{Bmatrix}_{2} = \begin{Bmatrix} +0.003473+j0.045270 \\ -0.003707-j0.016358 \end{Bmatrix}_{2}

很显然，模态向量不再是纯实数了。在两个模态向量中，不管如何对模态向量进行归一化，现在也需要用复数向量来描述模态向量。对于任意具有非比例阻尼的系统，情况都是这样。

上面的模态向量可以转化为幅值和相位。

因此，对第1阶模态向量：

\begin{Bmatrix} \psi_{1} \\ \psi_{2}\end{Bmatrix}_{1} = \begin{Bmatrix} 0.050220, \; -93.96^{\circ}\\ 0.058877, \; -86.39^{\circ} \end{Bmatrix}_{1}

对第2阶模态向量：

\begin{Bmatrix} \psi_{1} \\ \psi_{2}\end{Bmatrix}_{2} = \begin{Bmatrix} 0.045403, \; +85.61^{\circ}\\ 0.016765, \; -102.77^{\circ} \end{Bmatrix}_{2}

对模态1，跟前面的例子中一样，这两个质量几乎按同相运动。同样，对模态2，跟前面的例子中一样，这两个质量几乎按反相运动。因此，非比例阻尼系统，导致复模态振型，具有的相位项通常不是0^{\circ}或180^{\circ}。

另外一种比较实模态向量和复模态向量间区别的方法如下：实模态向量表示的振动模态，结构上的所有点同时通过它们的平衡位置。复模态向量表示的振动模态，结构上的点不在同一时刻通过其平衡位置。换句话讲，相对于结构，实模态像是驻波，复模态像是行波。实模态的节点或节线相对于结构，是静态的；相反，复模的节点或节线相对于结构不是静止的。

很多被测结构具有近乎实模态的振型，也即，相位项非常接近0^{\circ}或180^{\circ}。通常结构可以同时具有实模态振型和复模态振型。在前面的例子中，第1阶模态向量在\pm\,4^{\circ}内，几乎完全是实模态，而第2阶模态向量在\pm\,13^{\circ}内，接近实模态。因此，第2阶模态向量比第1阶模态向量要更复杂些。

5.4.1 脉冲响应函数示例

按照跟比例阻尼系统类似的方式来计算脉冲响应函数。根据式5.27，脉冲响应函数的基本定义为：

h_{pq}(t) = \textbf{L}^{-1}\biggl\{X_{p}(s)\biggr\} = \textbf{L}^{-1}\biggl\{\displaystyle\sum_{r=1}^{N} \dfrac{A_{pqr}}{(s-\lambda_{r})} + \dfrac{A_{pqr}^{*}}{(s-\lambda_{r}^{*})}\biggr\} \qquad (5.33)

现在，仅有的差别在于留数A_{pqr}不再是纯虚数了，却通常为复数。对一个两自由度系统，脉冲响应函数变为：

h_{pp}(t) = \textbf{L}^{-1}\biggl\{X_{p}(s)\biggr\} = A_{pp1}\,e^{\lambda_{1}t} + A_{pp1}^{*}\,e^{\lambda_{1}^{*}t}+ A_{pp2}\,e^{\lambda_{2}t}+ A_{pp2}^{*}\,e^{\lambda_{2}^{*}t} \quad (5.34)

具有复模态向量的系统（式5.34）和具有实模态向量的系统（式5.29和式5.30）的脉冲响应函数之间仅有的差异在于：每阶振动模态对于总体脉冲响应函数的个体贡献在零时刻不再是从零响应开始。注意，对于因果系统，这些个体贡献之和在零时刻必须为零。另外也注意到，留数，它跟输入自由度、响应自由度的模态系数的乘积成比例，显示为阻尼衰减正弦函数的幅值。

一个典型的频响函数，按照实部、虚部的方式再一次展示在图5-11中。这个频响函数H_{12}(\omega)代表在自由度2处对系统施加激励所引起的自由度1处的系统响应。图5-12是图5-11的等价的脉冲响应函数。类似的，这个脉冲响应函数h_{12}(t)代表在自由度2处对系统施加单位脉冲激励引起的自由度1处的系统响应。图5-11画的是一个具有复模态向量的两自由度系统的频响函数。此图与图5-4间仅有的差异在于：本例中的留数有非0^{\circ}或180^{\circ}的相位角。这个系统的脉冲响应函数如图5-12所示。注意，脉冲响应函数在t=0时刻的确是从零起始的。对于任意的因果系统，不管有还是没有复模态向量，情况都是这样。注意，尽管对于这种复模态向量的情况，来自于每一阶独立模态的脉冲响应函数贡献不从零起始。不过，对于一个因果系统，留数之和，故而，式5.27中的幅值和相位角求和在一起，将总是产生在0时刻幅值为零的脉冲响应函数。（对于任意系统，只要分子多项式的阶数比分母多项式的阶数低2阶或低更多阶，则留数之和为零）。同前，图5-11所示的频响函数是两个单自由度系统之和（图5-13和5-15）。对于这样一个简单的系统，复模态向量的另外一种指示是频响函数虚部的非对称特性。在图5-6和图5-8中，注意，虚部是对称的；而在图 5-13和图5-15中，虚部是不对称的。它们不对称的程度是模态向量特定元素如何复杂的一种指示。图5-14和图5-16分别是图5-13和图5-15的脉冲响应函数。

对于在所有例子中用到的这个简单的两自由度系统，现在可以比较无阻尼、比例阻尼和非比例阻尼系统的模态矢量和模态频率。记住，在所有例子中，刚度和质量是相同的。因此，模态向量和模态频率不同只是由于阻尼因素不同导致的。为比较起见，针对每种情况，根据传递函数标准形式得到的没有归一化的留数将用作模态向量。

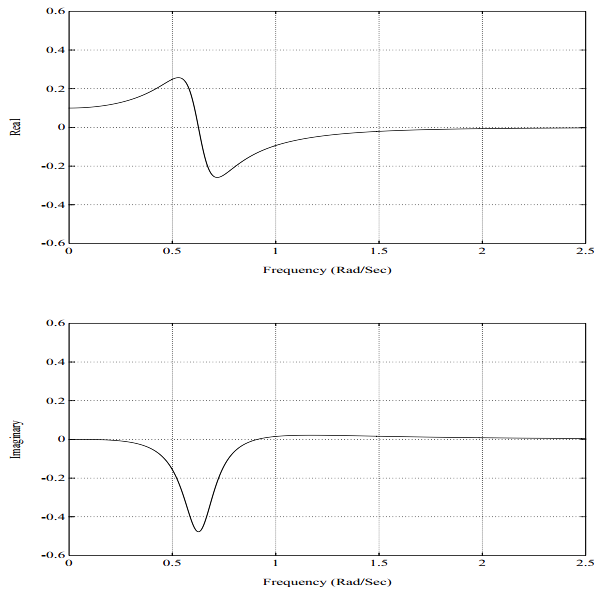
图5-11. 频响函数，2自由度系统，非比例阻尼

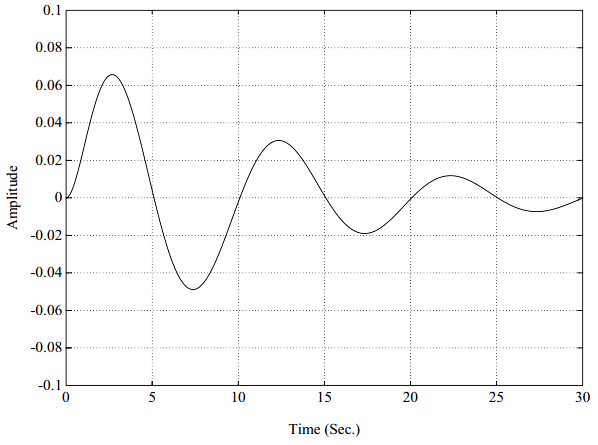
图5-12. 脉冲响应函数，2自由度系统，非比例阻尼

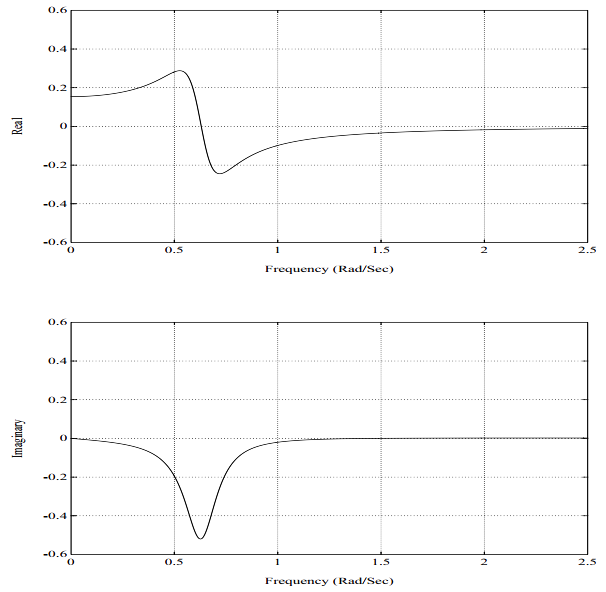
图5-13. 脉冲响应函数，2自由度系统，非比例阻尼，第1阶模态

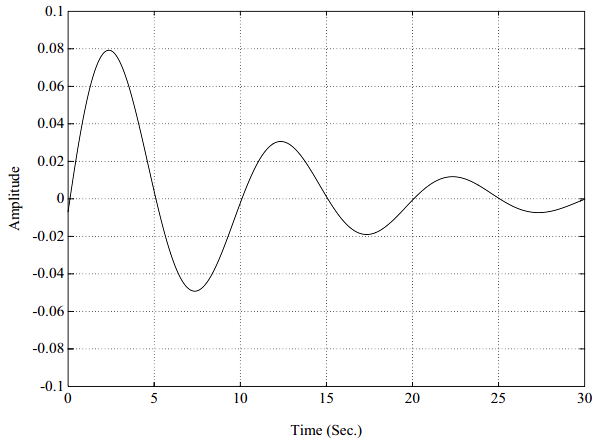
图5-14. 脉冲响应函数，2自由度系统，非比例阻尼，第1阶模态

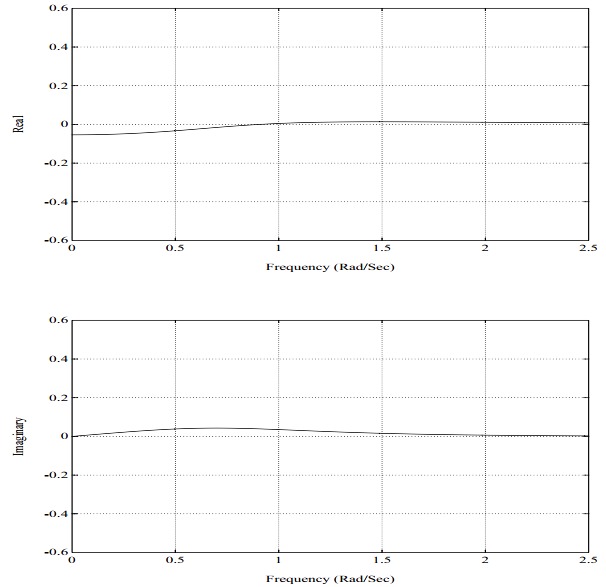
图5-15. 频响函数，2自由度系统，非比例阻尼，第2阶模态

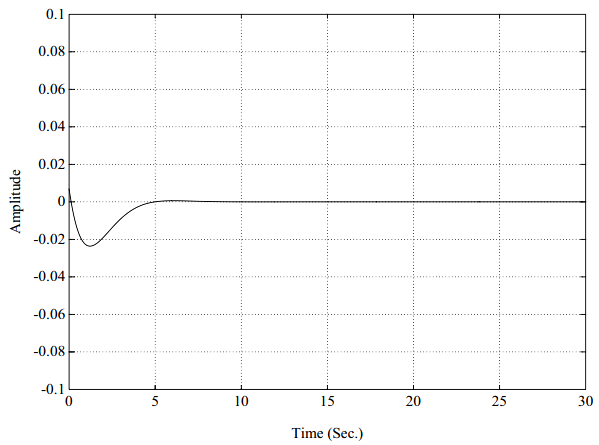
图5-16. 脉冲响应函数，2自由度系统，非比例阻尼，第2阶模态

5.5 模态参数（无阻尼和阻尼系统）总结

记得前面例子中的模态向量：

\qquad模态1 \qquad 模态2

无阻尼情况：

\begin{aligned} \lambda_{1}&= j \sqrt{2/5} \qquad \;\, \quad \qquad \lambda_{2} = j \\ \\ \psi_{1} &= \begin{Bmatrix} -j \dfrac{\sqrt{2/15}}{12} \\ -j \dfrac{\sqrt{2/15}}{12} \end{Bmatrix} \qquad \psi_{2} = \begin{Bmatrix} -j \dfrac{1}{15} \\ j \dfrac{1}{15} \end{Bmatrix} \end{aligned}

比例阻尼情况：

\begin{aligned} \lambda_{1}&= \dfrac{1}{10}+ j \bigl (\dfrac{\sqrt{39}}{10} \bigr)\;\; \,\quad \qquad \lambda_{2}= -\dfrac{1}{4}+ j \bigl (\dfrac{\sqrt{15}}{4} \bigr) \\ \\ \psi_{1} &= \begin{Bmatrix} -j \dfrac{\sqrt{39}}{117} \\ -j \dfrac{\sqrt{39}}{117} \end{Bmatrix} \qquad \; \qquad \psi_{2} = \begin{Bmatrix} -j \dfrac{4\sqrt{15}}{225} \\ j \dfrac{2\sqrt{15}}{225} \end{Bmatrix} \end{aligned}

非比例阻尼情况：

\begin{aligned} \lambda_{1}&= 0.095363+ j 0.629494 \; \,\quad \qquad \quad \qquad \lambda_{2}= -0.754635+ j0.645996 \\ \\ \psi_{1} &= \begin{Bmatrix} -0.008569-j0.041970 \\ -0.003473-j0.050100 \end{Bmatrix} \qquad \qquad \psi_{2} = \begin{Bmatrix} 0.008569-j 0.122700 \\ 0.003473+j0.045270 \end{Bmatrix} \end{aligned}

注意，对于非比例阻尼情况，表中给出的留数是针对相同的频响函数而言的（频响函数矩阵的第1列），频响函数应用于无阻尼和比例阻尼两种情况。这要求计算H_{11}(s)的留数。

记得，极点(\lambda_r)可写为：

\lambda_{r} = \sigma_{r}+j \omega_{r} = (- \zeta_{r}+ j \sqrt{1-\zeta_{r}^{2}})\Omega_{r} \qquad(5.35)

其中：

根据式5.35，也可以得到下面的关系：

\begin{aligned} \zeta_{r} &= \dfrac{-\sigma_{r}}{\sqrt{\omega_{r}^{2}+\sigma_{r}^{2}}} \\ \Omega_{r}&=\dfrac{-\sigma_{r}}{\zeta_{r}} \end{aligned}

现在，对于这3种不同的情况，可以比较第1阶模态向量。注意，模态向量已经转换为幅值、相位。

对模态向量1(\lambda_{1})：

无阻尼\qquad\qquad\qquad比例阻尼\qquad\qquad\qquad非比例阻尼

\begin{matrix} \begin{Bmatrix} 0.052705,\, -90^ {\circ}\\ 0.052705,\, -90^ {\circ} \end{Bmatrix} & \begin{Bmatrix} 0.053376,\, -90^ {\circ}\\ 0.053376,\, -90^ {\circ} \end{Bmatrix} & \begin{Bmatrix} 0.042836,\, -101.53^ {\circ}\\ 0.050220,\, -93.96^ {\circ} \end{Bmatrix} \\ \\ \Omega_{1}=0.632456& \Omega_{1}=0.632456 & \Omega_{1}=0.63667 \\ \\ \zeta_{1}=0\% & \zeta_{1}=15.8114\% & \zeta_{1}=14.9782\% \end{matrix}

对模态向量2(\lambda_{2})：

无阻尼\qquad\qquad\qquad比例阻尼\qquad\qquad\qquad非比例阻尼

\begin{matrix} \begin{Bmatrix} 0.06667,\, -90^ {\circ}\\ 0.033333,\, +90^ {\circ} \end{Bmatrix} & \begin{Bmatrix} 0.068853,\, -90^ {\circ}\\ 0.034427,\, +90^ {\circ} \end{Bmatrix} & \begin{Bmatrix} 0.122999,\, -86.00^ {\circ}\\ 0.045403,\, +85.61^ {\circ} \end{Bmatrix} \\ \\ \Omega_{1}=1.0 & \Omega_{1}=1.0 & \Omega_{1}=0.99377 \\ \\ \zeta_{1}=0\% & \zeta_{1}=25\% & \zeta_{1}=75.9671\% \end{matrix}

总之，注意对任何模态向量，加上阻尼（比例和无比例）对无阻尼固有频率没有影响。情况总是如此。进一步讲，模态向量的总体行为保持不变。也即，在第1阶模态中，两个质量按相同方向运动，而在第2阶模态中，它们按相反方向运动。主要的差别在于模态振型的相位。注意，对于非比例阻尼系统，相位项不再是0^{\circ}或180^{\circ}。这类模态也被称为复模态。相位与0^{\circ}或180^{\circ}相差多远与系统质量、阻尼和刚度分布直接相关。注意，对于某阶模态，只要相位接近0^{\circ}或180^{\circ}，通过令相位等于0^{\circ}或180^{\circ}，那么模态向量就可以用实模态或正则模态来近似。

上一章 第4章 频响函数推导 – 振动：解析与试验模态分析

下一章 第6章 频响函数合成 – 振动：解析与试验模态分析

返回《振动：解析与试验模态分析》中文翻译目录

扩展阅读[new]：
《模态空间系列文章》Peter Avitabile教授(著) KSI科尚仪器 董书伟 (译)…

《振动：试验模态分析》辛辛那提大学Randall J. Allemang教授(著) KSI科尚仪器 董书伟(译)…[new]