MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界 Pete Avitabile(著) KSI科尚仪器董书伟(译)
我仍然对所有模态的东西感到茫然未知。
拉普拉斯,傅里叶、频响,所有这一切!
你能为我汇总一下重点吗?
当然没有问题 … 有时它可以帮助我们往后站,从一幅完整的画面来观察一切。我有一幅图,用了很多年,现在可以帮助我们更清楚地看清事物。我称之为“重点图”。让我们看看这幅图,并单独讨论图中的各个部分吧。
首先,从一个解析表达式,如所示的有限元模型FEM开始入手。大致说来,利用FEM来近似描述通过弹簧互相联系在一起的一个集中质量系统,以表示物理系统。因为对于系统中描述的每个质量,根据力平衡方程来描述这种解析近似,所以最后对每个质量(或自由度)得到一个方程,用以近似描述这个系统。因为需要很多非常小的微元来精确描述系统,所以最后得到了很多方程,有很多未知数。可以很方便地马上用矩阵来描述所有这些方程。现在,一旦将所有这些方程组织在一起后,就可以利用一个称为特征解的数学形式,按照几个更简单的项 — 系统频率和模态振型,来表示系统 。这就是在有限元方法中我们所做的事情。
好了,不去深究所有细节,我可以得到那些相同的方程,并且将它们变换到拉氏域。(没有 — 我们没有切换到让你的生活充满痛苦的拉氏域 — 做变换是为了让某些方程更易于处理。这一点,请相信我!)现在,在拉氏域得到了系统方程[B(s)]以及它的逆矩阵[H(s)],也即系统传递函数。现在我们知道,这个逆矩阵是系统矩阵的伴随矩阵(或系统矩阵的余因子矩阵)除以系统矩阵的行列式。在所有的振动教科书中,都会介绍这个逆矩阵(通常在附录A)。
没什么大不了的!对你来说这意味着什么!嗯,结果证明伴随矩阵含有模态振型,而且我们称之为留数矩阵。[B(s)]的行列式含有系统的根,或称系统的极点。好了,这跟得自于解析模型的基本信息是一模一样。所以,我既可以根据解析模型,也可以根据拉氏域表达式,来确定系统的动力学特性 — 这二者将给出相同的结果。
现在,另一个重要的关系式是频响函数FRF。它是系统传递函数沿jω轴求值。FRF实际上是一个矩阵形式的项,[H(jω)]。嗯,因为我们正在处理矩阵,所以用下标来标识输入-输出测量结果会很方便。因此,‘j’测点处的输入激励引起的‘i’测点处的一个特定响应称为hij (jω)。
现在记住,目前为止系统传递函数是根据质量、阻尼、和刚度物理量来定义的。对任意的输入-输出组合,在任意想得到的频带范围内,都可以计算或综合出这个函数。所以,如果我们想要,我们就能够综合出一些FRFs,组成所需要的或想要得到的FRF矩阵的一个完整的行或一个完整的列,如图所示。
现在我们需要认识到的是,这些生成的(综合而来的)FRFs含有与系统特性相关的信息。记住,FRFs可以根据留数和极点来生成。另外,留数与振型直接相关,而极点是系统的频率和阻尼。
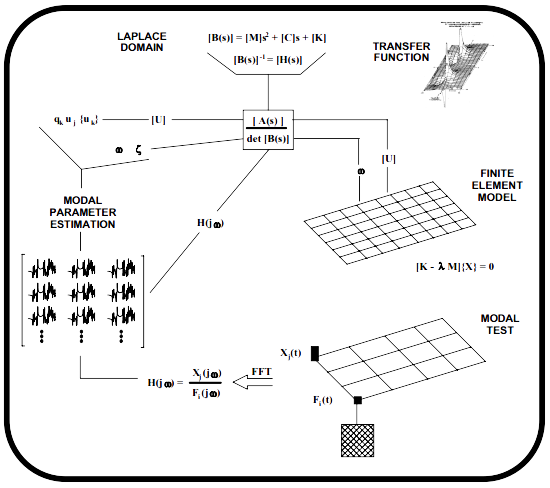
所以,组成FRFs的参数就是我们希望从FRFs中提取出来的参数。这就是模态参数估计的全部内容所在。大致说来,我们在数学算法中利用FRFs来提取组成FRF的基本信息 — 频率、阻尼、和模态振型。常常称这个过程为曲线拟合。提取出来的基本信息是模态振型,它与包含在伴随矩阵或留数矩阵里的信息相关;以及极点,它与系统矩阵的行列式里的信息相关。
这很好地总结了这个过程 — 除了一个重要的需要解决的问题之外。目前为止,我们只讨论了利用质量、阻尼、和刚度近似项,根据有限元模型或者根据系统拉氏域表达式来计算系统特性。这两种方法都是利用质量、阻尼、和刚度这些物理参数的近似项来描述系统,因此,它们将提供相同的基本信息。如果能有不需假定物理属性的其他方法来估计这些FRFs,那我就能够利用模态参数估计技术来提取想要得到的信息。
这就是模态试验的由来。总的说来用某种可测的激振力去激励结构。测量作用力引起的系统响应,与此同时测量激振力。现在利用FFT将这个时域数据转换到频域,大致说来计算得到输出响应与输入激振力的比值来形成一个FRF的近似。
进行这些测量有很多含意,它包含的数字信号处理的概念太多,多到现在不能立即进行详尽的讨论(但是根据这些内容,我认为你知道我将要讲什么)。
所以基于这个方法,我们能够测量某个输入-输出FRF。如果利用激振器来激励结构,并且移动加速度计到很多测点位置,就能测得了FRF矩阵的一列。(如果利用锤击技术来采集数据,那么能够测得FRF矩阵的一行)。所以进行测量的巨大优势在于,我测量作用力引起的结构响应 — 我并没有对系统的质量、阻尼、和刚度作任何假设 — 并且避免了可能做出的任何错误近似。当然要确保得到非常好的测量结果,否则会对系统特性造成失真。
因此,我希望这个讨论为你澄清了某些东西。如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:11. 模态空间99.10 — 我听说皮特现在不加窗函数了!怎么回事?
下一篇:13. 模态空间00.02 — 我展示振型给人看,他们问我结构设计的好吗?
![]()
延伸阅读[new]: 《振动:解析与试验模态分析》辛辛那提大学教授Randall J. Allemang博士 编著 KSI科尚仪器 董书伟 翻译…