MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Peter Avitabile(著) KSI科尚仪器董书伟(译)

我听说皮特现在不加窗函数了!怎么回事?
嗯…情况就是那样子。但是你得让我说明那个说法是对的。当然,有很多数据采集的情况必须要施加窗函数。但是,进行模态试验时,在几乎所有的时候,都能够选择输入激励,这样就不用施加窗函数。我们首先了解为什么量化和采样过程会造成某些类型的数据采集发生失真?需要做些什么以减少失真?另外如何通过选择专门的试验激励技术来解决这个采集问题?
首先,我们记住,傅里叶变换是在-∞到+∞上定义的,但是,我们只能采集很短的一段时间范围内的数据。从测量的这个非常短的样本中,只要我们都能够重构所有时间的数据,那就没有问题。
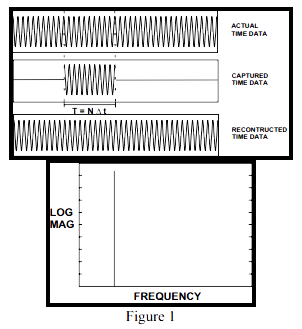
图1显示了一个简单的正弦波、采样到的一段时间记录、从样本点中重建的时域信号。图1同时显示了采样到的信号的FFT结果。如同我们所期待的那样,时域信号在频域内表现为一根离散的谱线。出现这种情况是因为在一次数据记录或样本中,采集到了整数周期的正弦波形 — 在这种情况下,我们说,信号相对于采样时间段是周期的。
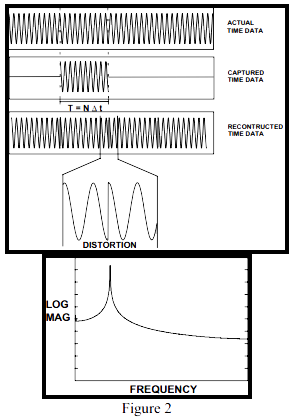
但如果情况并非如此,又会怎样呢?图2说明了这种情况。跟以前一样,我们观察这个信号、样本数据、重建的信号、和信号的FFT结果。注意到,重建信号包含不连续点,显然,它们在原始信号中并不存在。这个信号的FFT结果远不是我们所期望的那样为一根谱线。因为采样失真,频域表现形式在整个频带范围内发生了模糊。这个非常严重的误差称为泄漏,并且是目前为止,我们遇到的最为严重的数字信号处理误差。
但为什么会发生这种情况呢?原始信号原先是一个简单的正弦波。为什么频域表现形式变得如此失真?对此有一个简单的解释。采样到的数据没有包含整数周期的,或反复发生的信号。
停下来,回忆一下我们学过的关于傅里叶级数的某些简单内容。如果从简单的正弦波开始,我们知道,用傅里叶级数来描述这个信号是一个很简单的任务。从根本上讲,它只是傅里叶级数中的一项,它是一个频率为ω、幅值为A0的正弦波。但是,你还记得一个信号,如矩形脉冲序列,的级数展开式是什么吗?好了,此刻,我不想对这些内容进行全面展开,但是,我认为你应该记得,它是一系列不同的频率上、具有不同幅值的正弦波。实际上,对于矩形脉冲,为了逼近这个信号,在级数中,需要有很多项。这种情况的发生是因为不连续的矩形脉冲的形状看起来不像一个很好的光滑的正弦波。
现在,如果我回过头来观察图2中采样到的正弦波,可以发现,由于没有采集到整数周期的信号,使得信号发生了失真,这样在信号采样时间段的末端,信号看起来具有不连续点。这解释了为什么FFT在整个频带范围内发生了模糊。从根本上讲,需要有很多项来逼近这个明显不连续的信号。
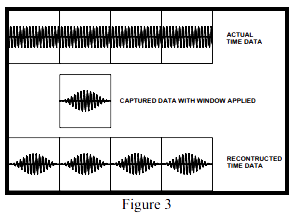
为了将这个误差减至最小(并且注意我的说是减至最小,而不是消除),我们使用称为窗的加权函数。从根本上讲,我们施加一个加权函数来使得信号看起来更好地满足FFT处理的周期性要求。图3显示了一个加窗后的时域波形。
今天,对于模态试验来讲,最常见的窗函数,对激振器试验,是矩形窗、汉宁窗、和平顶窗,而对锤击试验,是力窗/指数窗。在刚开始时,需要了解的主要一点是,所有的窗函数都会造成数据失真!不去深究所有细节,在测得的FRF中,窗函数总是使测得的峰的幅度发生失真,总是给出好像更大的阻尼,比实际存在的阻尼要大 — 这两个是我们试图从所测的函数中估计出来的非常重要的特性。对矩形窗,最大失真可至36%,对汉宁窗,最大失真可至16%。这些窗函数的影响最好在加权函数的频域表现形式中观察。所有的窗函数都具有一个特征形状,可以识别出可能的幅值失真的程度、带来的阻尼影响、和可能的信息模糊的程度。图4显示出了矩形窗、汉宁窗、和平顶窗的频域表现形式。很快在某个时候我们会更深入地讨论这些曲线是什么意思,但是,目前你只要知道窗函数会造成数据畸变,我就很高兴了,在某些测量情况下,窗是我们不愿做,却又不得不做的事。

那么对模态试验,我该怎么避免对测量的FRF施加窗函数呢?从根本上讲,我要尽量满足傅里叶的要求 — “或者采样一段重复的信号,或者在一个数据样本中可以完整地观察到信号”。思考一下这点,在大多数条件下,诸如伪随机、猝发随机、正弦扫频、和数字步进正弦的信号都满足这个要求,因而没有泄露,不需要加窗。下一次,我们或许可以讨论每个窗函数的特点。但是目前来讲,这个非常简短的解释应该足够了。
现在,我希望你理解了为什么我不喜欢使用窗了,而且我将不惜一切代价地避免使用窗 — 但我时常又没有其他选择。(特别是在家里,我从来都逃不掉“擦窗”!)如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:10. 模态空间99.08 — 你确信可以从频响H矩阵的一行或者一列得到模态振型吗?当然确信无疑!
下一篇:12. 模态空间99.12 — 我仍然对所有模态的东西感到茫然未知。拉普拉斯、傅立叶、频响、所有这一切!
![]()
延伸阅读[new]: 《振动:解析与试验模态分析》辛辛那提大学教授Randall J. Allemang博士 编著 KSI科尚仪器 董书伟 翻译…