MODAL SPACE – IN OUR OWN LITTLE WORLD
模态空间 – 在我们自己的小世界中 Pete Avitabile(著) KSI科尚仪器 董书伟(译)

如何解释稳态图?另外数据点如何影响拟合?
这里有些概念很重要,要讨论一下
2014年06月01日 发布 ver1.0
参数估计过程是模型(极点和留数)提取的一个非常重要的部分。通常这被分解成两个部分 – 在第一步中提取极点,接下来在第二步中估计留数。稳态图是一种工具,用在从数据中提取留数的过程中。我们讨论一下极点的估计和稳态图的使用。这里包含几个简单的例子来让你彻底理解估计过程中的关键问题点。
我们假设有一组数据,如图1所示。作为起点,将假定一个三阶拟合来很好地描述这个现象。总体上,很大的R2系数表明这种拟合是合理的。但是当包含误差容限时(点线),可以允许有一定的变动量。显然可以看到一个点是数据拟合的异常点。如果从数据组中去掉这个异常点,如图2所示,那么R2系数增加。那么根据此处所示的这组数据,非常清楚地说明,数据质量对于提取一组有效的参数是非常重要的。拥有高质量的数据对于估计过程是极端重要的。
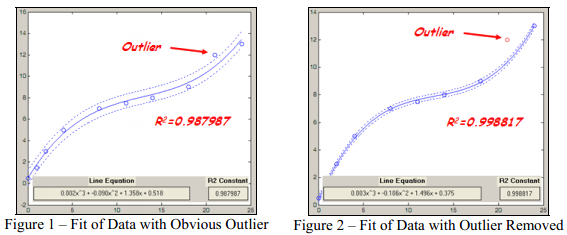
图1 – 带有明显异常点的数据拟合 图2 – 去掉异常点的数据拟合
根据这个简单的例子,显然,良好的数据非常重要。现在考虑图3所示的数据。这是非常简单的一组数据,看起来具有非常简单的一阶特性。随着模型的阶数增加,我们研究估计出的参数。

图3 – 一组相当线性的数据

图4a – 数据的一阶拟合 图4b – 数据的二阶拟合
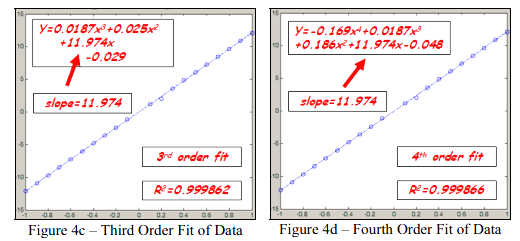
图4c – 数据的三阶拟合 图4d – 数据的4阶拟合
图4中的图形显示了随着模型阶数从1阶增长到4阶,斜率估计的演变。图4a中,一阶拟合得到一个13.097的斜率、一个很好的R2值。现在随着模型阶数增长到2阶,斜率仍然是12.097,R2值不错。所以模型阶数增加到2阶没有产生斜率估计上的变化。当然,一般地,对更高的阶数项进行调整来解释所测数据上的变化。
随着模型阶数增加到3阶,斜率是11.974,非常接近于先前根据1阶和2阶模型计算出来的斜率。实际上,斜率只有1%的区别。所以我们可以认为斜率基本相同,离之前的估计没有大的改变。并且随着阶数模型进一步增加到4阶模型,斜率再一次估计为11.974,没有改变。
所以这个过程完成之后,普遍的共识将是数据的斜率参数大约是12.0,随着模型阶数增加,极少发生改变。另外注意到,我用什么阶数的模型无关紧要,因为误差在1%之内。所有的阶数得到了基本相同的斜率。
这个简单的例子确实提供了稳态图形成幕后所发生事情的确切理解。随着模型阶数增加,将有极点的估计。如果从一个模型阶数到下一个模型阶数,估计出的极点只是改变了很少一点,那么软件将提供一个标识(或指示符)来帮助理解极点是否达到了某种“稳定值”,在某种规定容限之内。(为了确定极点的稳定性,这些容限对频率可能设置为1%,阻尼为5%。)通常将提供一些指示符号,被叠加到SUM,MMIF 或CMIF图上。作为参考一个典型的稳态图如图5所示。稳态图帮助确定随着模型阶数增加,哪些极点是“一致的”或稳定的。
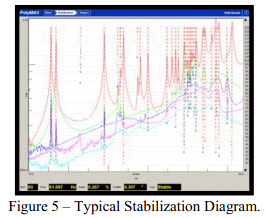
图5 – 典型的稳态图
如果你有关于模态分析的任何其他问题,尽管问我好了。
![]()
上一篇:56. 模态空间07.04 – 你如何选择模态试验的参考点位置?需要考虑什么?
下一篇:58. 模态空间07.08 – 稳态图具有MMF或CMIF没有指示出的极点。它们真的是模态吗?
![]()
扩展阅读[new]:
《振动:解析与试验模态分析》辛辛那提大学 Randall J. Allemang教授(著) KSI科尚仪器 董书伟(译)…